前言
生活所迫(x
分组密码,又称块加密
参考:
https://ctf-wiki.org/crypto/blockcipher/introduction/
《现代密码学(第5版)》—— 杨波
分组密码概述
参考: https://blog.csdn.net/m0_62396648/article/details/131319813
将明文划分为长为n的组x(x0,x1,…,xn-1),各组在密钥k=(k0,k1,…kt-1)控制下变换成等长的数字序列y=(y0,y1,…ym-1)
实际上就是对字长为n的数字序列的代换密码(一般m=n)
分组密码安全设计性原则:
- 扩散:使明文与密文之间的统计关系变得尽可能复杂,以使敌手无法得到密钥。明文每一比特变换尽量多的影响密文序列的变化,以隐蔽明文的统计特性(雪崩效应)
- 混淆:使密文与密钥之间的统计关系变得尽可能复杂,以使敌手无法得到密钥
P盒(置换)用于扩散
S盒(代换)用于混淆
Feistel结构
Feistel提出利用乘积密码可以获得简单的代换密码,”乘积密码“指顺序地执行两个或多个基本密码系统,使得最后结果的密码强度高于每个基本密码系统产生的结果,Feistel还提出了实现代换和置换的方法。
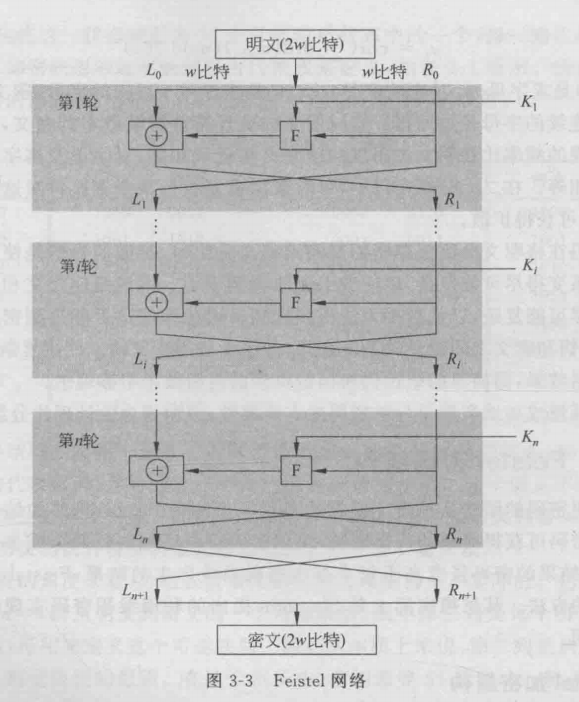
分成左右两边,右边用 F 进行加密,和左边异或一下,和这一轮原始的进行交换,进行n轮迭代,最后置换一下,再合在一起
DES
参考: https://blog.csdn.net/jayq1/article/details/132380018
基本操作:
- 输入 64 位。
- 输出 64 位。
- 密钥 64 位,使用 64 位密钥中的 56 位,剩余的 8 位要么丢弃,要么作为奇偶校验位。
- Feistel 迭代结构
- 明文经过 16 轮迭代得到密文。
- 密文经过类似的 16 轮迭代得到明文。
密钥产生:
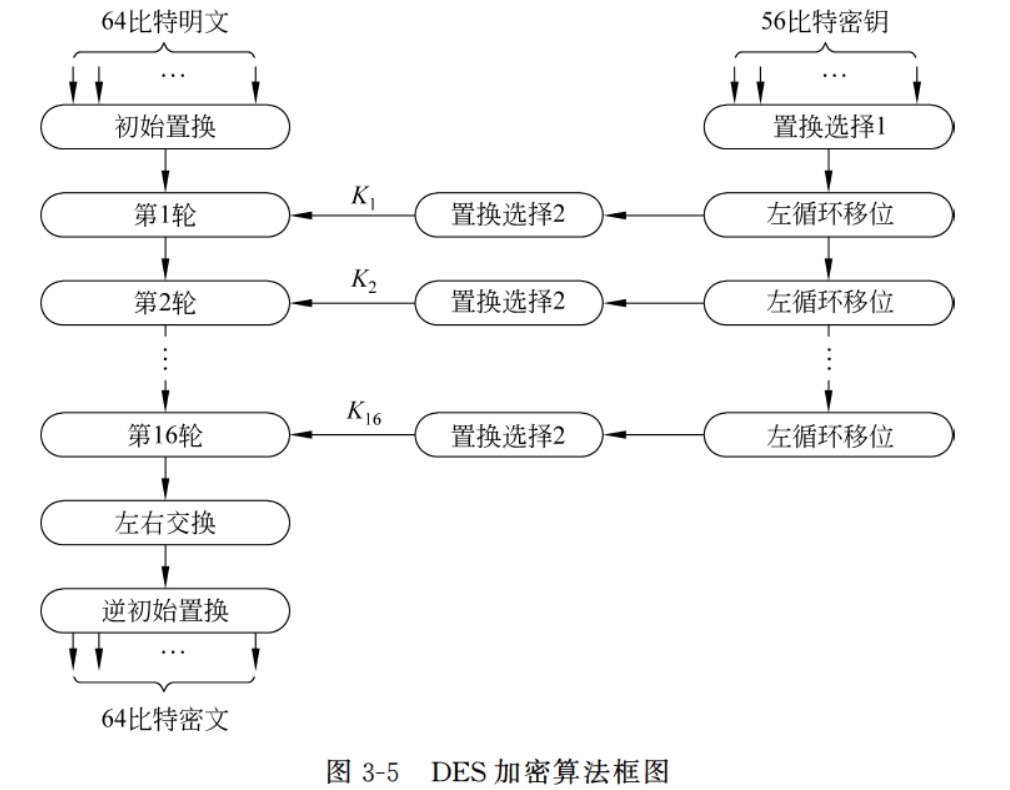
初始置换
将64bits的待加密数据块进行排列,形成IP盒
然后对IP进行一系列操作
将第58个比特放在第一个位置上,逆初始置换也一样,第40个比特放在第一个位置上(即对照IP盒和IP-1盒进行置换)
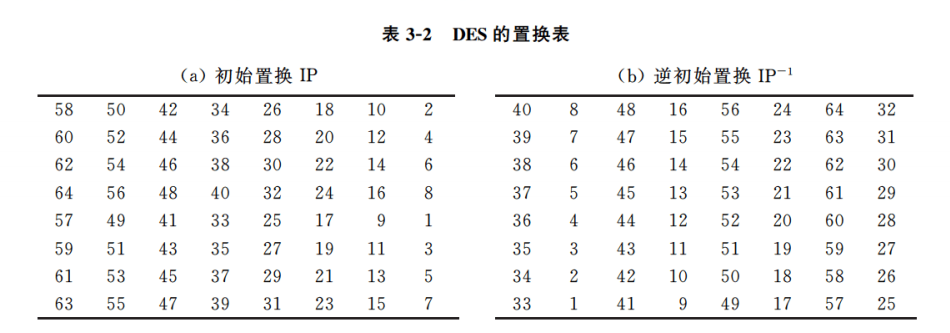
轮结构
将数据切割成左右两部分
Ln=Rn-1
Rn=Ln-1 ^ f(Rn-1,Kn)
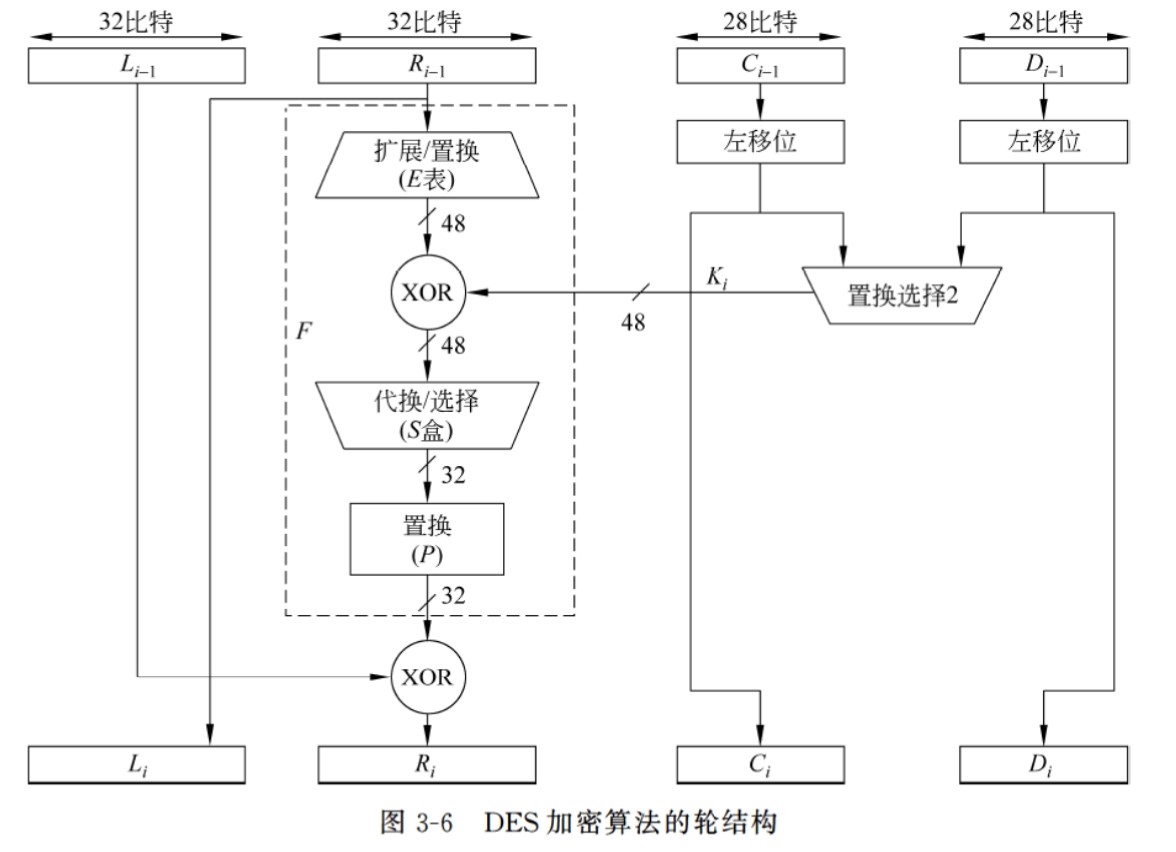
将右边的32比特扩展到48比特,与48比特的密钥Ki进行轮密钥加,得到48比特长的结果再通过S盒压缩到32比特,通过置换得到32比特长的轮函数输出,再与左边进行一次异或,得到本次的R结果,一轮就结束了
扩展运算:对照E盒的位置,把四个,边上的前一个和后一个扩展了。如左上角第一个取第32比特
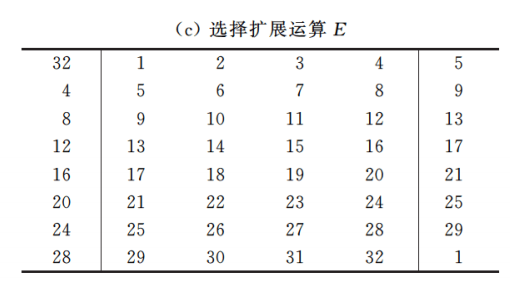
轮密钥加:把8组6比特变成4比特,具体操作就是把6比特输入看成一个二进制数,16位选行,2-4选列,然后查S盒
密钥加密流程
首先对 KEY 进行排列,每8bit删除最后一个(奇偶校验位),然后根据PC-1盒(8行7列共56个)生成相应位置的数值,再进行左移位,对照PC-2盒产生Kn
来一个demo:
原始的64bit KEY:0001001100110100010101110111100110011011101111001101111111110001
转换成类似矩阵的线性排列
0 0 0 1 0 0 1 1 #8
0 0 1 1 0 1 0 0 #16
0 1 0 1 0 1 1 1 #24
0 1 1 1 1 0 0 1 #32
1 0 0 1 1 0 1 1 #40
1 0 1 1 1 1 0 0 #48
1 1 0 1 1 1 1 1 #56
1 1 1 1 0 0 0 1 #64然后根据 PC-1 盒里对应位置的数值选择对应位置交换
比如第1位是57,则置换之后的结果的第1位就是KEY中的第57位,即0 -> 1
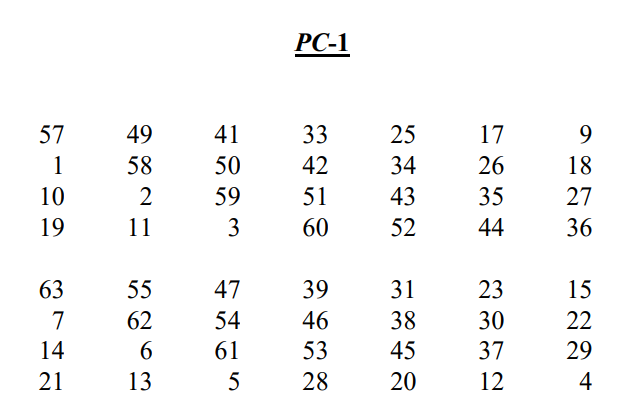
逐个替换,最后得到结果:
1 1 1 1 0 0 0
0 1 1 0 0 1 1
0 0 1 0 1 0 1
0 1 0 1 1 1 1
----------------------
0 1 0 1 0 1 0
1 0 1 1 0 0 1
1 0 0 1 1 1 1
0 0 0 1 1 1 1此时只剩下56位
然后取前四行为C,后四行为D
依靠固定的移位表

而此时
C0 = 1111000011001100101010101111
D0 = 0101010101100110011110001111
为了获得C1,就按照1去查找,表中对应的左移位为1,这里举个左移2位的的例子:
原始:1,2,3,4,……,27,28
左移:3,4,5,6,……,28,1,2
所以C1 = 1110000110011001010101011111
同理D1 = 1010101011001100111100011110
接下来根据PC-2提取Kn
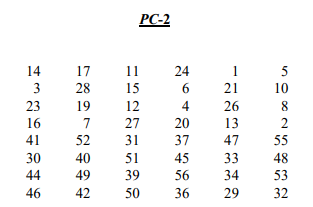
这里可以说明 Kn 的第一位是 CnDn 组合中的第14位,即 0
所以K1 = 000110110000001011101111111111000111000001110010
逆推子密钥
代码实现
参考: https://blog.csdn.net/weixin_44034444/article/details/121055630
import binascii
class DES():
def __init__(self):
# 初始化DES加密的参数
self.ip = [
58, 50, 42, 34, 26, 18, 10, 2, 60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6, 64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1, 59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5, 63, 55, 47, 39, 31, 23, 15, 7,
] # ip置换
self.ip1 = [
40, 8, 48, 16, 56, 24, 64, 32, 39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30, 37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28, 35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26, 33, 1, 41, 9, 49, 17, 57, 25,
] # 逆ip置换
self.E = [
32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1,
] # E置换,将32位明文置换位48位
self.P = [
16, 7, 20, 21, 29, 12, 28, 17,
1, 15, 23, 26, 5, 18, 31, 10,
2, 8, 24, 14, 32, 27, 3, 9,
19, 13, 30, 6, 22, 11, 4, 25,
] # P置换,对经过S盒之后的数据再次进行置换
self.K = ''
self.k1 = [
57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4,
] # 密钥的K1初始置换
self.k2 = [
14, 17, 11, 24, 1, 5, 3, 28,
15, 6, 21, 10, 23, 19, 12, 4,
26, 8, 16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55, 30, 40,
51, 45, 33, 48, 44, 49, 39, 56,
34, 53, 46, 42, 50, 36, 29, 32,
]
self.k0 = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1, ] # 秘钥循环移位的位数
self.S = [
[
14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13
],
[
15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9
],
[
10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12
],
[
7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14
],
[
2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3
],
[
12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13
],
[
4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12
],
[
13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11
],
] # 16进制表示S盒的数据,S盒是为了将48位转换为32位,有8个盒子
def __substitution(self, table: str, self_table: list) -> str:
"""
:param table: 需要进行置换的列表,是一个01字符串
:param self_table: 置换表,在__init__中初始化了
:return: 返回置换后的01字符串
"""
sub_result = ""
for i in self_table:
sub_result += table[i - 1]
return sub_result
def str2bin(self, string: str) -> str:
"""
将明文转为二进制字符串:
:param string: 任意字符串
:return:二进制字符串
"""
plaintext_list = list(bytes(string, 'utf8')) # 将字符串转成bytes类型,再转成list
result = [] # 定义返回结果
for num in plaintext_list:
result.append(bin(num)[2:].zfill(8)) # 将列表的每个元素转成二进制字符串,8位宽度
return "".join(result)
def bin2str(self, binary: str) -> str:
"""
二进制字符串转成字符串
:param binary:
:return:
"""
list_bin = [binary[i:i + 8] for i in range(0, len(binary), 8)] # 对二进制字符串进行切分,每8位为一组
list_int = []
for b in list_bin:
list_int.append(int(b, 2)) # 对二进制转成int
result = bytes(list_int).decode() # 将列表转成bytes,在进行解码,得到字符串
return result
def __bin2int(self, binary: str) -> list:
"""
由于加密之后的二进制无法直接转成字符,有不可见字符在,utf8可能无法解码,所以需要将二进制字符串每8位转成int型号列表,用于转成bytes再转hex
:param binary: 二进制字符串
:return: int型列表
"""
list_bin = [binary[i:i + 8] for i in range(0, len(binary), 8)] # 对二进制字符串进行切分,每8位为一组
list_int = []
for b in list_bin:
list_int.append(int(b, 2))
return list_int
def __int2bin(self, list_int: list) -> str:
result = []
for num in list_int:
result.append(bin(num)[2:].zfill(8))
return ''.join(result)
def __get_block_list(self, binary: str) -> list:
"""
对明文二进制串进行切分,每64位为一块,DES加密以64位为一组进行加密的
:type binary: 二进制串
"""
len_binary = len(binary)
if len_binary % 64 != 0:
binary_block = binary + ("0" * (64 - (len_binary % 64)))
return [binary_block[i:i + 64] for i in range(0, len(binary_block), 64)]
else:
return [binary[j:j + 64] for j in range(0, len(binary), 64)]
def modify_secretkey(self):
"""
修改默认密钥函数
:return: None
"""
newkey = input("输入密钥(长度为8):")
if len(newkey) != 8:
print("密钥长度不符合,请重新输入:")
self.modify_secretkey()
else:
bin_key = self.str2bin(newkey)
self.K = bin_key
print("当前二进制形式密钥为:{}".format(self.K))
def __f_funtion(self, right: str, key: str):
"""
:param right: 明文二进制的字符串加密过程的右半段
:param key: 当前轮数的密钥
:return: 进行E扩展,与key异或操作,S盒操作后返回32位01字符串
"""
# 对right进行E扩展
e_result = self.__substitution(right, self.E)
# 与key 进行异或操作
xor_result = self.__xor_function(e_result, key)
# 进入S盒子
s_result = self.__s_box(xor_result)
# 进行P置换
p_result = self.__substitution(s_result, self.P)
return p_result
def __get_key_list(self):
"""
:return: 返回加密过程中16轮的子密钥
"""
key = self.__substitution(self.K, self.k1)
left_key = key[0:28]
right_key = key[28:56]
keys = []
for i in range(1, 17):
move = self.k0[i - 1]
move_left = left_key[move:28] + left_key[0:move]
move_right = right_key[move:28] + right_key[0:move]
left_key = move_left
right_key = move_right
move_key = left_key + right_key
ki = self.__substitution(move_key, self.k2)
keys.append(ki)
return keys
def __xor_function(self, str1: str, str2: str):
"""
:param str1: 01字符串
:param str2: 01字符串
:return: 异或操作返回的结果
"""
result = ""
for i in range(0, len(str1)):
if str1[i] == str2[i]:
result += "0"
else:
result += "1"
return result
def __s_box(self, xor_result: str):
"""
:param xor_result: 48位01字符串
:return: 返回32位01字符串
"""
result = ""
for i in range(0, 8):
# 将48位数据分为6组,循环进行
block = xor_result[i * 6:(i + 1) * 6]
line = int(block[0] + block[5], 2)
colmn = int(block[1:5], 2)
res = bin(self.S[i][line*16 + colmn])[2:]
if len(res) < 4:
res = '0' * (4 - len(res)) + res
result += res
return result
def __iteration(self, bin_plaintext: str, key_list: list):
"""
:param bin_plaintext: 01字符串,64位
:param key_list: 密钥列表,共16个
:return: 进行F函数以及和left异或操作之后的字符串
"""
left = bin_plaintext[0:32]
right = bin_plaintext[32:64]
for i in range(0, 16):
next_lift = right
f_result = self.__f_funtion(right, key_list[i])
next_right = self.__xor_function(left, f_result)
left = next_lift
right = next_right
bin_plaintext_result = left + right
return bin_plaintext_result[32:] + bin_plaintext_result[:32]
def encode(self, plaintext):
"""
:param plaintext: 明文字符串
:return: 密文字符串
"""
bin_plaintext = self.str2bin(plaintext)
bin_plaintext_block = self.__get_block_list(bin_plaintext)
ciphertext_bin_list = []
key_list = self.__get_key_list()
for block in bin_plaintext_block:
# 初代ip置换
sub_ip = self.__substitution(block, self.ip)
ite_result = self.__iteration(sub_ip, key_list)
# 逆ip置换
sub_ip1 = self.__substitution(ite_result, self.ip1)
ciphertext_bin_list.append(sub_ip1)
ciphertext_bin = ''.join(ciphertext_bin_list)
result = self.__bin2int(ciphertext_bin)
return bytes(result).hex().upper()
def decode(self, ciphertext):
'''
:param ciphertext: 密文字符串
:return: 明文字符串
'''
b_ciphertext = binascii.a2b_hex(ciphertext)
bin_ciphertext = self.__int2bin(list(b_ciphertext))
bin_plaintext_list = []
key_list = self.__get_key_list()
key_list = key_list[::-1]
bin_ciphertext_block = [bin_ciphertext[i:i + 64] for i in range(0, len(bin_ciphertext), 64)]
for block in bin_ciphertext_block:
sub_ip = self.__substitution(block, self.ip)
ite = self.__iteration(sub_ip, key_list)
sub_ip1 = self.__substitution(ite, self.ip1)
bin_plaintext_list.append(sub_ip1)
bin_plaintext = ''.join(bin_plaintext_list).replace('00000000', '')
return self.bin2str(bin_plaintext)
def main(self):
select = input("Please selecting:\n1、Encryption\t 2、Decrpytion\t 3、Exit\nYour selecting:")
if select == '1':
plaintext = input("Input plaintext:")
# print("Your plaintext is:{}".format(plaintext))
ciphertext = self.encode(plaintext)
print("The ciphertext is:{}".format(ciphertext))
elif select == '2':
plaintext = input("Input ciphertext:")
# print("Your ciphertext is:{}".format(plaintext))
plaintext = self.decode(plaintext)
print("The plaintext is:{}".format(plaintext))
# print(len(plaintext))
elif select == '3':
exit()
else:
input("Please selecting again!")
self.main()
if __name__ == '__main__':
mydes = DES()
mydes.modify_secretkey()
while True:
mydes.main()
print("")分组模式
ECB
电码本模式(Electronic CodeBook)
一次对一个64bit长的明文分组加密,且每次都加密密钥都相同
用途:传送短数据(如一个加密密钥)
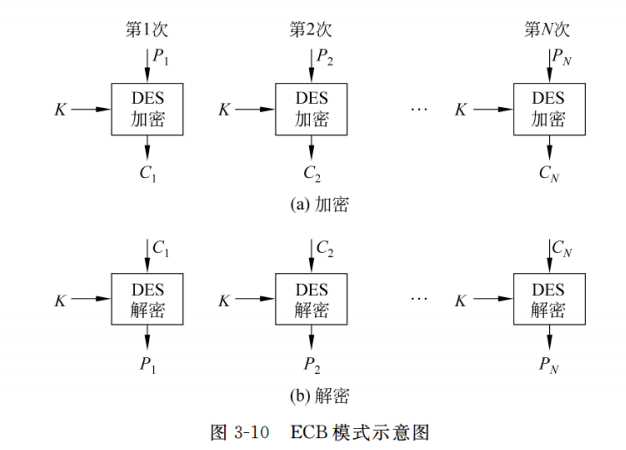
问题:同样的明文块会被加密成相同的密文块,不会隐藏明文分组的统计规律。类似于下图,相同的色块在加密后也呈现出相同的色块。即 ECB 会泄露数据的模式

CBC
密码分组链接模式(Cipher Block Chaining)
让重复的明文分组产生不同的密文分组
一次对一个明文分组加密,每次加密使用同一密钥,加密算法的输入是当前明文分组和前一次密文分组的异或
在产生第一个密文分组时,需要有一个初始向量 IV 与第一个明文分组异或;解密时,IV 和解密算法对第一个密文分组的输出进行异或以恢复第一个明文分组
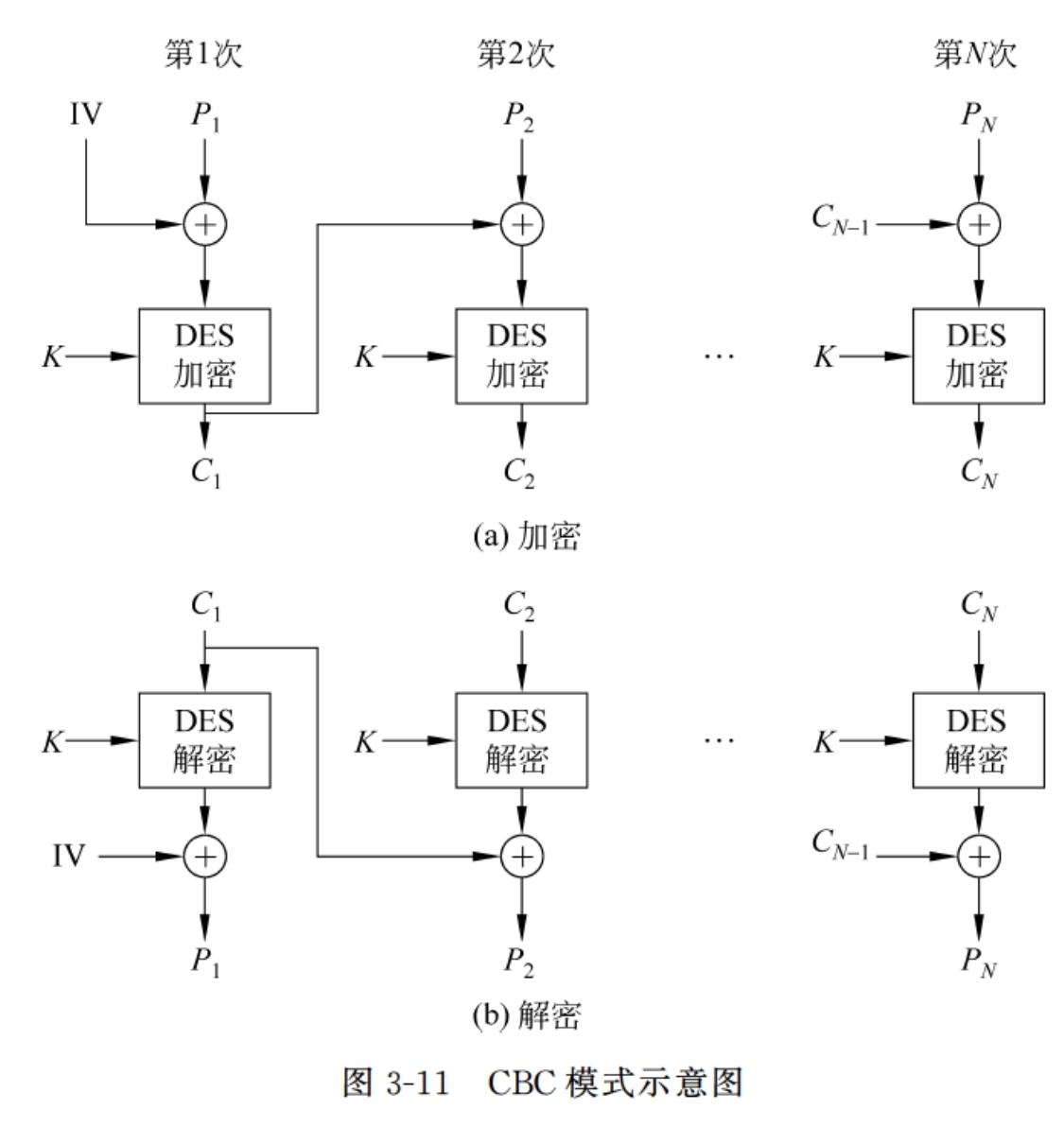
安全性:IV 应像密钥一样被保护。由图可知,一次加密中有地方出错后面所有的加密会全部出错;解密时,一次解密中有地方出错不会影响后面的解密
用途:传送数据分组(如加密文件);认证
攻击:字节反转攻击
观察解密过程可以发现如下特性:
- IV 向量影响第一个明文分组
- 第 n 个密文分组可以影响第 n + 1 个明文分组
假设第 n 个密文分组为Cn,解密后的第 n 个明文分组为为Pn
然后Pn+1=Cn xor f(Cn+1),其中 f 函数为上图的DES解密
对于某个信息已知的原文和密文,然后我们可以修改第 n 个密文块 Cn 为Cn xor Pn+1 xor A。然后再对这条密文进行解密,那么解密后的第 n 个明文块将会变成 A
CFB
密码反馈模式(Cipher FeedBack)
将DES转换为流密码
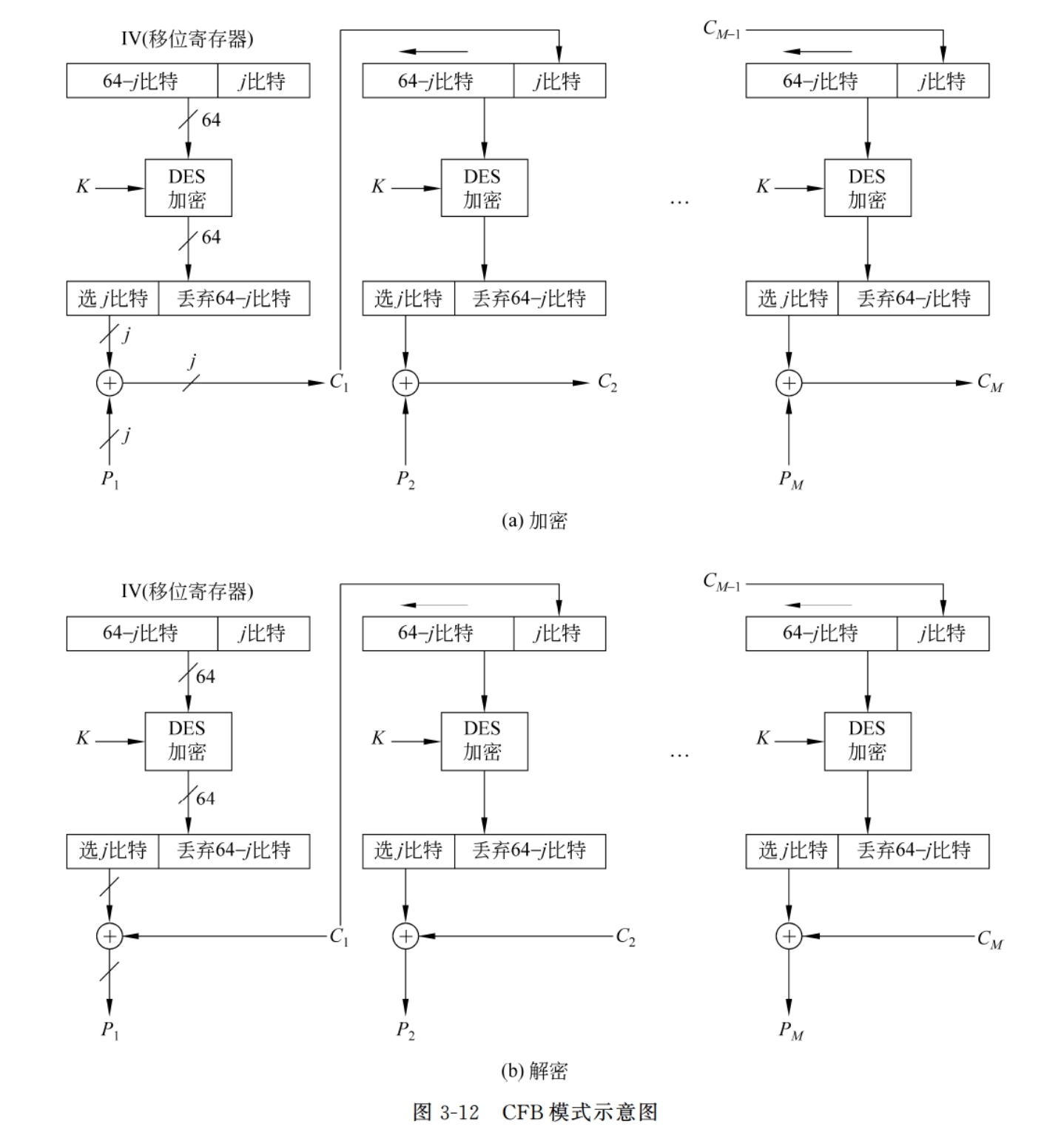
因为流密码具有密文和明文一样长的性质,所以如果需要发送的每个字符长为8bit,就应使用8bit密钥来加密每个字符,如果密钥长超过8bit,则造成浪费
错误恢复:j=8的情况下,
如果在一次加密中有地方出错,那么在接下来8次加密内会出错;但是会在第9次之后恢复正常,错误的bit位均被丢弃
如果在一次解密中有密文分组出错,那么初始向量的移位寄存器中会出错,导致在后面的8个分组均会出错,第10个分组开始恢复正常
用途:传送数据流;认证
OFB
输出反馈模式(Output FeedBack)
OFB模式是将加密算法的输出反馈到移位寄存器,而CFB模式是将密文单元反馈到移位寄存器
因此,有密文分组出错的时候,OFB传输过程中的bit错误不传播
IV 无需保密,但是对每个消息必须选择不同的 IV
安全性:比CFB更容易受到消息流的篡改攻击
用途:适用于一些明文冗余度比较大的场景,如有扰信道上(如卫星通信)传送数据流
IDEA
国际数据加密算法(International Data Encryption Algorithm,IDEA)
AES
高级加密标准(Advanced Encryption Standard),又称Rijndael加密法
输入:128bit
输出:128bit
AES的分组长度是128bit,有三种可选的密钥长度128bit、192bit和256bit,轮数分别为10、12和14
数学基础
域上运算
有限域GF(28):有限个元素的域,这里是28个
多项式表示法:
例:57+83=D4,
用多项式表示为:(x6+x4+x2+x+1)+(x7+x+1) = x7+x6+x4+x2
用二进制表示为:01010111 + 10000011 = 11010100
注:由于每个元素的加法逆元等于自己,所以减法和加法相同
要计算GF(28)上的乘法,必须先确定一个GF(2)上的8次不可约多项式;则在GF(28)上两个元素的乘积就是这两个多项式的模乘(以这个8次不可约多项式为模)
在AES中,这个8次不可约多项式为:m(x) = x8+x4+x3+x+1,16进制表达为 11B
例:57*83 = C1
多项式表示:(x6+x4+x2+x+1)*(x7+x+1) = x7+x6+1 (mod m(x))
以上定义的乘法满足交换律,且有单位元01。另外,对任何次数小于8的多项式b(x),可用推广的欧几里得算法得:b(x)a(x)+m(x)c(x) = 1,即a(x)*b(x) = 1 mod m(x),因此 a(x) 是 b(x) 的乘法逆元。再者,乘法还满足分配律
所以,256bits构成的集合,在以上定义的加法和乘法运算下,有有限域GF(28)的结构
x乘法:x * b(x) = b7x8+b6x7+…+b1x2+b0x (mod m(x))
状态、种子密钥和轮数
状态:算法的中间结果也需分组,称算法中间结果的分组为状态,所有的操作都在状态上进行
种子密钥:用一个以字节为元素的矩阵阵列表示,该阵列有4行,列数记为Nk,Nk等于分组长度除以32
轮函数
由4个不同的计算部件组成:字节代换(ByteSub)、行移位(ShiftRow)、列混合(MixColimn)、密钥加(AddRoundKey)
字节代换
非线性变换,独立地对状态的每个字节进行
代换表(S盒):可逆,由以下两个变换的合成得到:
- 首先,将字节看作GF(28)上的元素,映射到自己的乘法逆元,00映射到自己
- 其次,对字节做(GF(2)上的,可逆的)仿射变换:ByteSub(State)
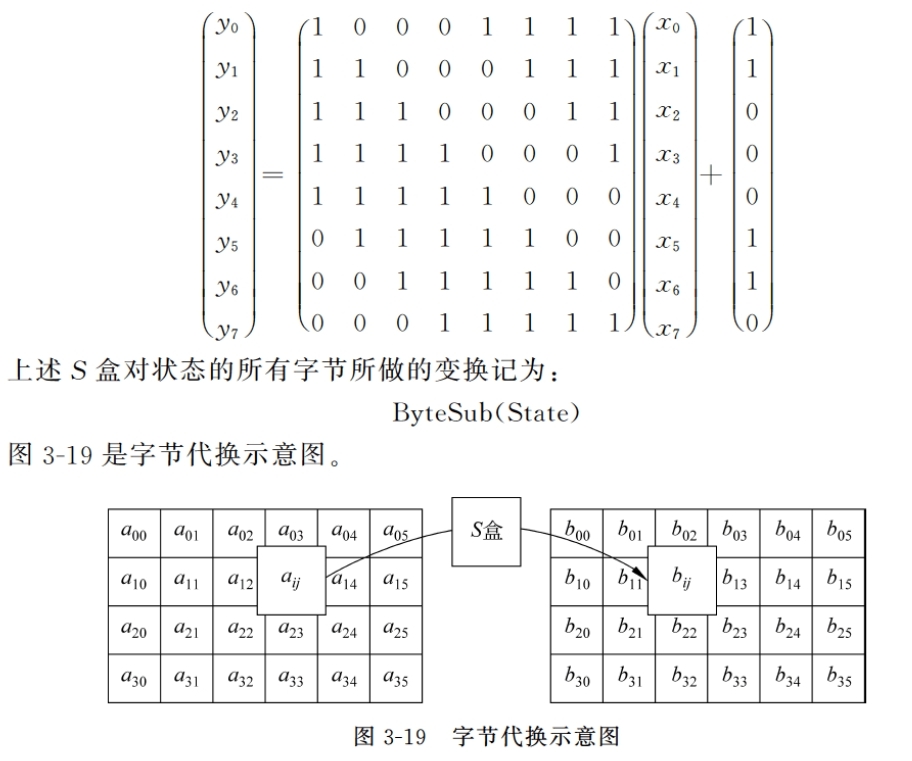
逆变换:先仿射逆变换,再求每个字节在GF(28)上的逆元
行移位
将状态阵列的各行进行循环移位,不同状态行的位移量不同
第0行不移动,第1行循环左移C1个字节,第2行循环左移C2个字节,第3行循环左移C3个字节
位移量的取值与Nb有关
| Nb | C1 | C2 | C3 |
|---|---|---|---|
| 4 | 1 | 2 | 3 |
| 6 | 1 | 2 | 3 |
| 8 | 1 | 3 | 4 |
行移位运算:ShiftRow(State)
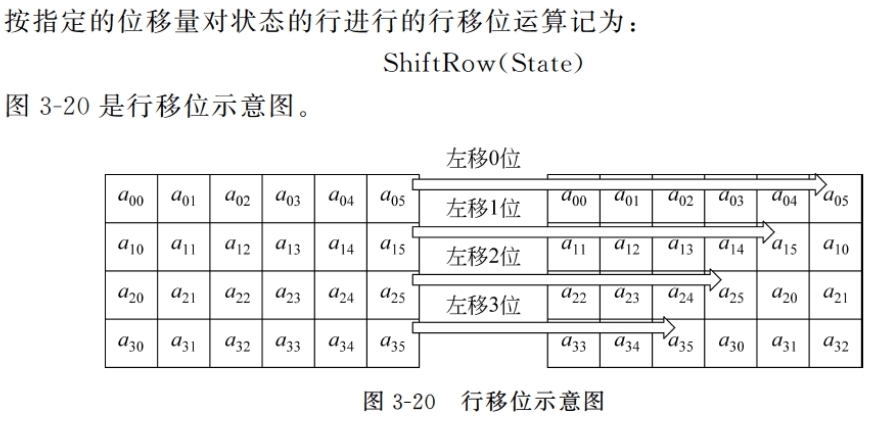
逆变换:对状态阵列的后3列分别以位移量 Nb-C1、…进行循环移位,使第i行第j列的字节移位到 (j + Nb - Ci)mod Nb
列混合
将状态阵列的每个列视为GF(28)上的多项式,再与一个固定的多项式 c(x) 进行模 x4+1 乘法
列混合运算:MixColumn(State)
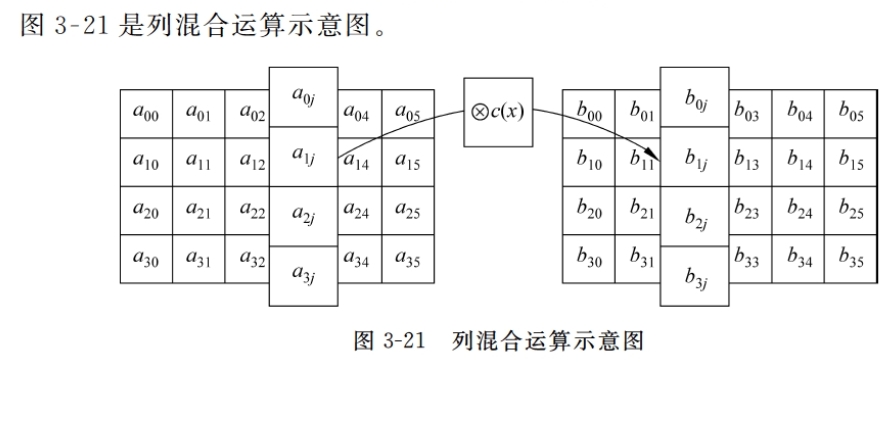
密钥加
将轮密钥简单地与状态进行逐比特异或
密钥加运算:AddRoundKey(State, RoundKey)
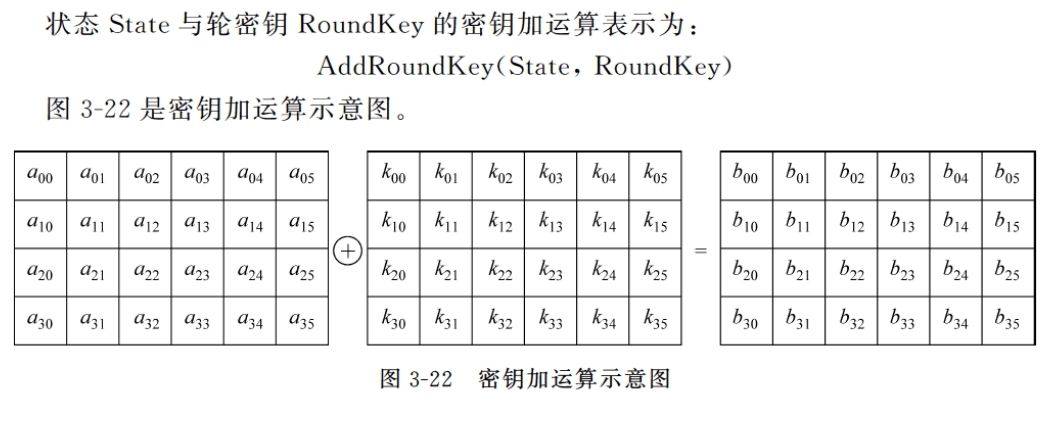
密钥编排
加密算法
加解密的相近程度及解密算法
先上结论:
设字节代换、行移位的逆变换分别为 InvByteSub、InvShiftRow,则组合部件 ByteSub -> ShiftRow 的逆变换为 InvByteSub -> InvShiftRow
设列混合的逆变换为 InvMixColumn ,则列混合部件与密钥加部件的组合部件 MixColumn -> AddRoundKey(State,Key) 的逆变换为 InvMixColumn -> AddRoundKey(State,InvKey)
有组合部件:
MixColumn(State); AddRoundKey(State,Key(i)); ByteSub(State); ShiftRow(State)其逆变换为:
InvByteSub(State); InvShiftRow(State); InvMixColumn(State); AddRoundKey(State,InvMixColumn(Key(i)))
