前言
https://www.runoob.com/w3cnote/bubble-sort.html
烂尾+2
冒泡排序
通过重复地遍历待排序的列表,比较相邻的元素并交换它们的位置来实现排序。
def bubble_sort(arr):
n = len(arr)
for i in range(n):
swap = False
print(i)
for j in range(0, n - i - 1): # 每轮排序后第n-i位一定比前面大
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
swap = True
if not swap:
break
return arr
arr = [5,7,2,1,3]
sorted_arr = bubble_sort(arr)
print(sorted_arr)
# 5,7,2,1,3
# 5,7,2,1,3
# 5,2,7,1,3
# 5,2,1,7,3
# 5,2,1,3,7
# 2,5,1,3,7
# 2,1,5,3,7
# 2,1,3,5,7
# 1,2,3,5,7选择排序
每次从待排序的数据中选择最小(或最大)的元素,放到已排序序列的末尾,直到全部数据排序完成
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_i = i
for j in range(i + 1, n):
if arr[j] < arr[min_i]:
min_i = j
arr[i], arr[min_i] = arr[min_i], arr[i]
return arr
arr = [54, 12, 3, 66, 22]
sorted_arr = selection_sort(arr)
print(sorted_arr)
# [54],12,3,66,22
# 54,[12],3,66,22
# 54,12,[3],66,22
# 54,12,[3],66,22
# 54,12,[3],66,22
# 3,12,54,66,22
# 3,[12],54,66,22
# ...插入排序
每步将一个待排序的对象,按其关键码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止
即边插入边排序,保证子序列中随时都是排好序的
直接插入排序
整个排序过程为n-1趟插入,即先将序列中第1个记录看成是一个有序子序列,然后从第2个记录开始,逐个进行插入,直至整个序列有序
例:(13,6,3,31,9,27,5,11)
[13], 6, 3, 31, 9, 27, 5, 11
[6, 13], 3, 31, 9, 27, 5, 11
[3, 6, 13], 31, 9, 27, 5, 11
[3, 6, 13,31], 9, 27, 5, 11
[3, 6, 9, 13,31], 27, 5, 11
[3, 6, 9, 13,27, 31], 5, 11
[3, 5, 6, 9, 13,27, 31], 11
[3, 5, 6, 9, 11,13,27, 31]折半插入排序
希尔排序
先将整个待排记录序列分割成若干子序列,分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序
注:子序列的构成不是简单地“逐段分割”,而是将相隔某个增量dk的记录组成一个子序列让增量dk逐趟缩短(例如依次取5,3,1)直到dk=1为止
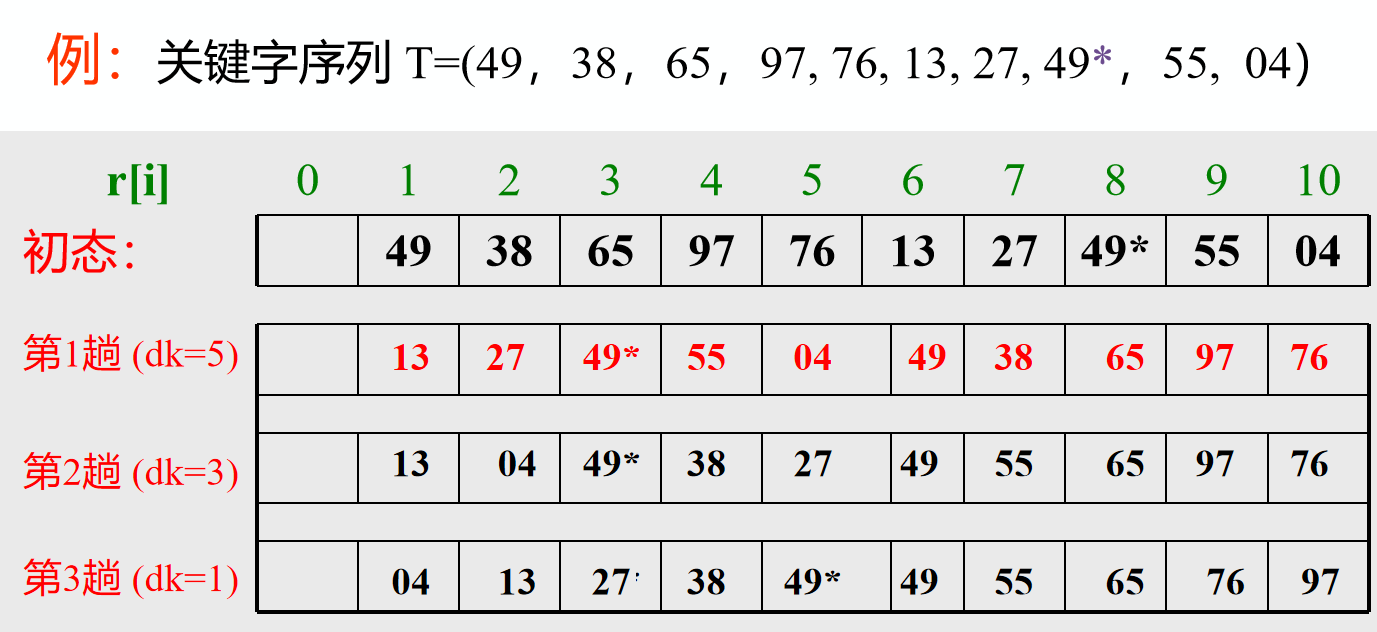
第1趟:16,27,38,49,5~10进行比较
第2趟:14,25,36,47,58,69,7~10进行比较
第3趟同理
交换排序
基本思想:两两比较,如果发生逆序则交换,直到所有记录都排好序为止
起泡排序
每趟不断将记录两两比较,并按“前小后大” 规则交换
快速排序
任取一个元素 (如第一个) 为中心
所有比它小的元素一律前放,比它大的元素一律后放,形成左右两个子表;
对各子表重新选择中心元素并依此规则调整,直到每个子表的元素只剩一个
选择排序
从未排序序列中挑选元素,并将其依次放入已排序序列(初始时为空)的一端
每一趟在后面 n - i +1 个中选出关键码最小的对象, 作为有序序列的第 i 个记录
简单选择排序
树形选择排序
堆排序
归并排序
将两个或两个以上的有序表组合成一个新有序表
