目录

  1. 1. 前言
  2. 2. 串
    1. 2.1. 定义
    2. 2.2. 存储结构
      1. 2.2.1. 顺序存储
      2. 2.2.2. 链式存储
    3. 2.3. 模式匹配
      1. 2.3.1. BF算法
      2. 2.3.2. KMP算法
  3. 3. 数组
  4. 4. 广义表
↑

LOADING

第一次加载文章图片可能会花费较长时间

要不挂个梯子试试？（x

加载过慢请开启缓存 浏览器默认开启

串、数组和广义表

2024/1/23 Basic 数据结构
字数统计: 1.5k字   |   阅读时长: 5分   |   总文章阅读量：次

前言

烂尾+3

串

定义

零个或多个字符组成的有限序列

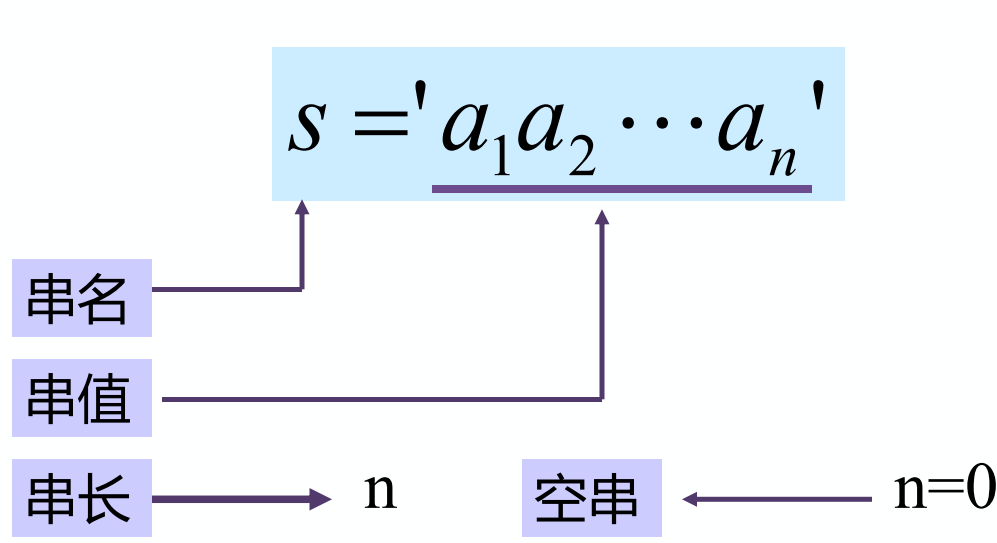
image-20240123004440392

  • 子串：串中任意个连续字符组成的子序列称为该串的子串

  • 主串：包含子串的串相应地称为主串

  • 字符位置：字符在序列中的序号为该字符在串中的位置

  • 子串位置：子串第一个字符在主串中的位置

  • 空格串：由一个或多个空格组成的串，与空串不同

  • 串相等：当且仅当两个串的长度相等并且各个对应位置上的字符相同时，这两个串才是相等的。(所有的空串是相等的)

  • 前缀：从串首开始到某个位置 i 结束的一个特殊子串

    字符串 abcabcd 的所有前缀为 {a, ab, abc, abca, abcab, abcabc, abcabcd}, 而它的真前缀为 {a, ab, abc, abca, abcab, abcabc}

  • 后缀：从某个位置 i 开始到整个串末尾结束的一个特殊子串

    字符串 abcabcd 的所有后缀为 {d, cd, bcd, abcd, cabcd, bcabcd, abcabcd}，而它的真后缀为 {d, cd, bcd, abcd, cabcd, bcabcd}

存储结构

顺序存储

用一组地址连续的存储单元存储串值的字符序列，类似于线性表的顺序存储结构

定长顺序存储结构：直接使用定长的字符数组来定义

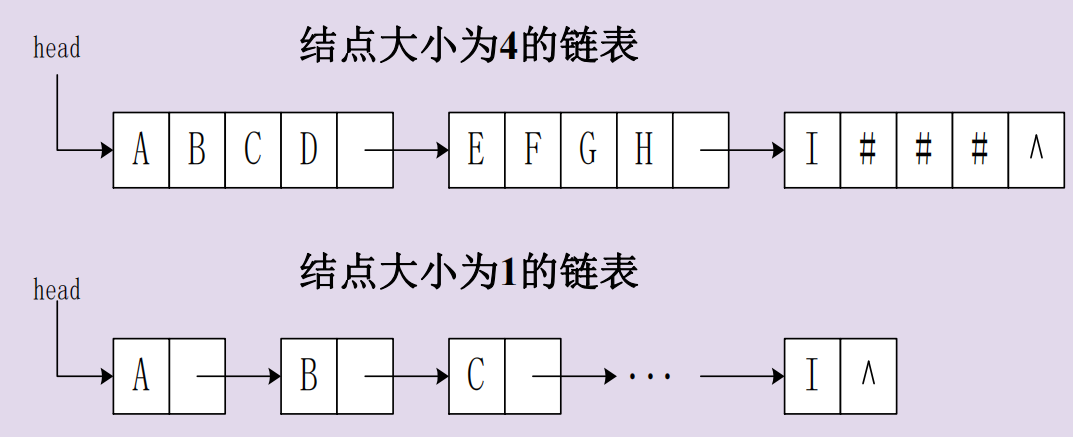
链式存储

以链表存储串值，除头指针外还可以附设一个尾指针指示链表中的最后一个结点，并给出当前串的长度

image-20240123005000569

模式匹配

确定主串中所含子串第一次出现的位置（定位）

BF算法

Index(S,T,pos)

将主串的第pos个字符和模式的第一个字符比较，

若相等，继续逐个比较后续字符；

若不等，从主串的下一字符起，重新与模式的第一个字符比较。

直到主串的一个连续子串字符序列与模式相等 。返回值为S中与T匹配的子序列第一个字符的序号，即匹配成功。

否则，匹配失败，返回值

KMP算法

参考：https://zq99299.github.io/dsalg-tutorial/dsalg-java-hsp/14/04.html#kmp-%E6%80%9D%E8%B7%AF%E5%88%86%E6%9E%90

利用已经部分匹配的结果而加快模式串的滑动速度

思路来源：

以下列字符串举例

Str1 = "BBC ABCDAB ABCDABCDABDE"
Str2 = "ABCDABD"

  1. 都用第 1 个字符进行比较，不符合，关键词（文本串）向后移动一位

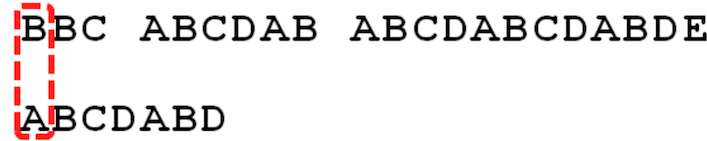
    image-20240123013816474

  2. 重复第一步，还是不符合，再后移动

    image-20240123013843721

  3. 一直重复，直到 str1 有一个字符与 str2 的第一个字符匹配为止

    image-20240123013854251

  4. 接着比较字符串和搜索词的下一个字符，还是符合

    image-20240123013905476

  5. 遇到 st1 有一个字符与 str2 对应的字符不符合时

    image-20240123013919298

  6. 这时候想到的是继续遍历 str1 的下一个字符（也就是暴力匹配）

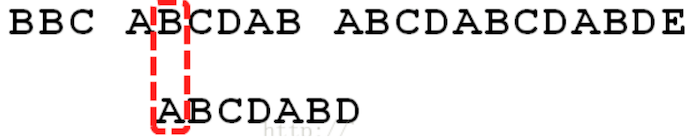
    image-20240123013935119

    但是此时会出现一个问题：

    image-20240123014004269

    此时回溯时，A 还会去和 BCD 进行比较，而在上一步 ABCDAB 与 ABCDABD，前 6 个都相等，其中 BCD 搜索词的第一个字符 A 不相等，那么这个时候还要用 A 去匹配 BCD，这肯定会匹配失败

而 KMP 算法的思想是：设法利用这个已知信息，不要把「搜索位置」移回已经比较过的位置，继续把它向后移，这样就提高了效率

那么问题来了，如何知道 A 与 BCD 不相同，并且只有 BCD 不用比较呢？

  1. KMP利用部分匹配表来省略掉刚刚重复的步骤：

    image-20240123014219797

    1. ABCD 匹配值 0

    2. ABCDA 匹配值 1

    3. ABCDAB 匹配值 2

那么继续刚才的步骤，

  1. 已知空格与 D 不匹配时，前面 6 个字符 ABCDAB 是匹配的

    查表可知：部分匹配值是 2，因此按照公式计算出后移的位数：移动位数 = 已匹配的字符数 - 对应的部分匹配值

    因此回溯的时候往后移动 4 位，而不是暴力匹配移动的 1 位

  2. 因为空格与 C 不匹配

    image-20240123014900217

    搜索词还要继续往后移动，这时，已匹配的字符数为 2 （AB），对应的 部分匹配值 为 0，所以 移动位数 = 2 - 0 = 2，于是将搜索词（文本串）向后移动两位

    image-20240123014938067

  3. 因为空格与 A 不匹配，继续往后移动一位

  4. 此时，部分匹配表已用完，需要一位一位进行匹配，直到发现 C 与 D 不匹配。于是，移动位数 = 6-2，继续将搜索词（文本串）往后移动 4 位

  5. 逐位比较，直到搜索词（文本串）的最后一位，发现完全匹配，搜索完成

    image-20240123015039975

部分匹配值就是前缀和后缀的最长的共有元素的长度，下面以 ABCDABD 来解释：

字符串 前缀 后缀 共有元素 共有元素长度
A - - - 0
AB A B - 0
ABC A、AB BC、C - 0
ABCD A、AB、ABC BCD、CD、D - 0
ABCDA A、AB、ABC、ABCD BCDA、CDA、DA、A A 1
ABCDAB A、AB、ABC、ABCD、ABCDA BCDAB、CDAB、DAB、AB、B AB 2
ABCDABD A、AB、ABC、ABCD、ABCDA、ABCDAB BCDABD、CDABD、DABD、ABD、BD、D - 0

next数组：

next[1]=0
next[2]=1
next[j]=从j-1开始，向前找相等的前缀和后缀的最长长度+1（找不到或前缀和后缀位于同一位置时为0）

nextval数组：

  1. 求next数组
  2. 遍历i，若i和next[i]对应的字符相同，那么赋值next[i]=next[next[i]]

例：给定字符串"ababaaababaa"，计算其next数组

(0) 前缀为""，后缀也是""，匹配长度0

(1) 前缀为"a"，后缀为""，匹配长度0

(2) 前缀为"ab"，后缀为""，匹配长度0

(3) 前缀为"aba"，后缀为"a"，匹配长度1

(4) 前缀为"abab"，后缀为"ab"，匹配长度2

(5) 前缀为"ababa"，后缀是"ba"，匹配长度0

数组

广义表