前言
烂尾+1
基本概念
- 查找表:由同一类型的数据元素(或记录)构成的集合
- 静态查找表:查找的同时对查找表不做修改操作(如插入和删除)
- 动态查找表:查找的同时对查找表具有修改操作
- 关键字:记录中某个数据项的值,可用来识别一个记录
- 主关键字:唯一标识数据元素
- 次关键字:可以标识若干个数据元素
常用操作:
- 查询某个“特定的”数据元素是否在查找表中
- 检索某个“特定的”数据元素的各种属性
- 在查找表中插入一个数据元素
- 从查找表中删去某个数据元素
关键字的平均比较次数,也称平均搜索长度ASL(Average Search Length)
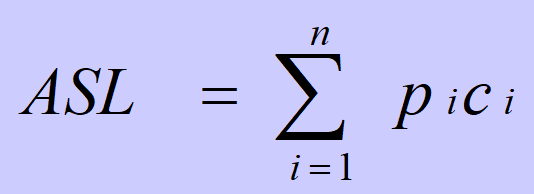
n:记录的个数
pi:查找第i个记录的概率 ( 通常认为pi =1/n )
ci:找到第i个记录所需的比较次数
线性表的查找
顺序查找(线性查找)
应用:顺序表或线性链表表示的静态查找表,表内元素之间无序
折半查找(二分查找)
仅适用于有序的顺序表
非递归算法:
设表长为n,low、high和mid分别指向待查元素所在区间的上界、下界和中点,k为给定值
初始时,令low=1,high=n,mid= (low+high)/2
让k与mid指向的记录比较
若k==R[mid].key,查找成功
若k<R[mid].key,则high=mid-1
若k>R[mid].key,则low=mid+1
重复上述操作,直至low>high时,查找失败
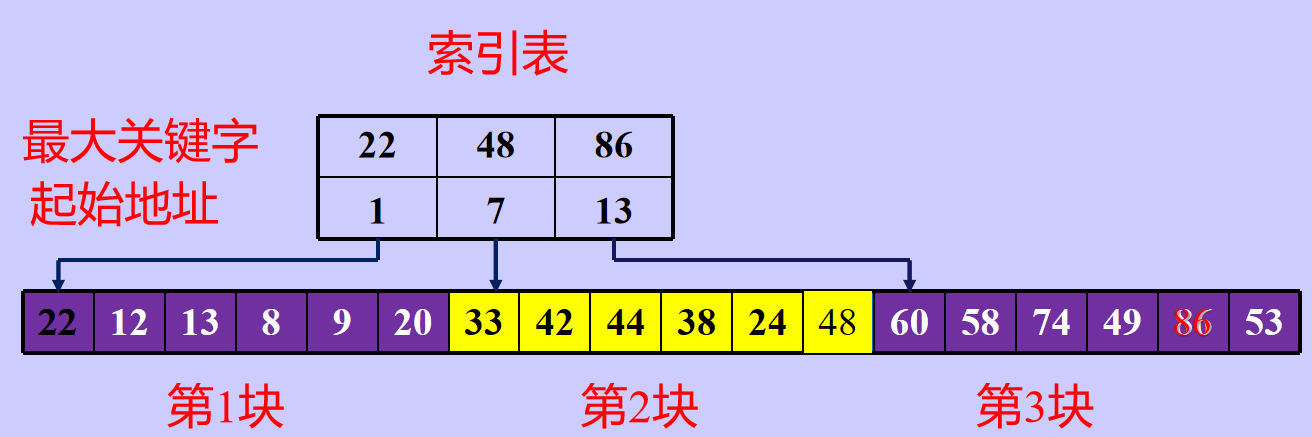
分块查找
块间有序,块内无序
即分成若干子表,要求每个子表中的数值都比后一块中数值小
树表的查找
表结构在查找过程中动态生成
对于给定值key,若表中存在,则成功返回;否则插入关键字等于key的记录
二叉排序树
空树 或 满足如下性质的二叉树:
若其左子树非空,则左子树上所有结点的值均小于根结点的值;
若其右子树非空,则右子树上所有结点的值均大于等于根结点的值;
其左右子树本身又各是一棵二叉排序树
查找
算法思想:
若二叉排序树为空,则查找失败,返回空指针
若二叉排序树非空,将给定值key与根结点的关键字T->data.key进行比较:
若key等于T->data.key,则查找成功,返回根结点地址;
若key小于T->data.key,则进一步查找左子树;
若key大于T->data.key,则进一步查找右子树
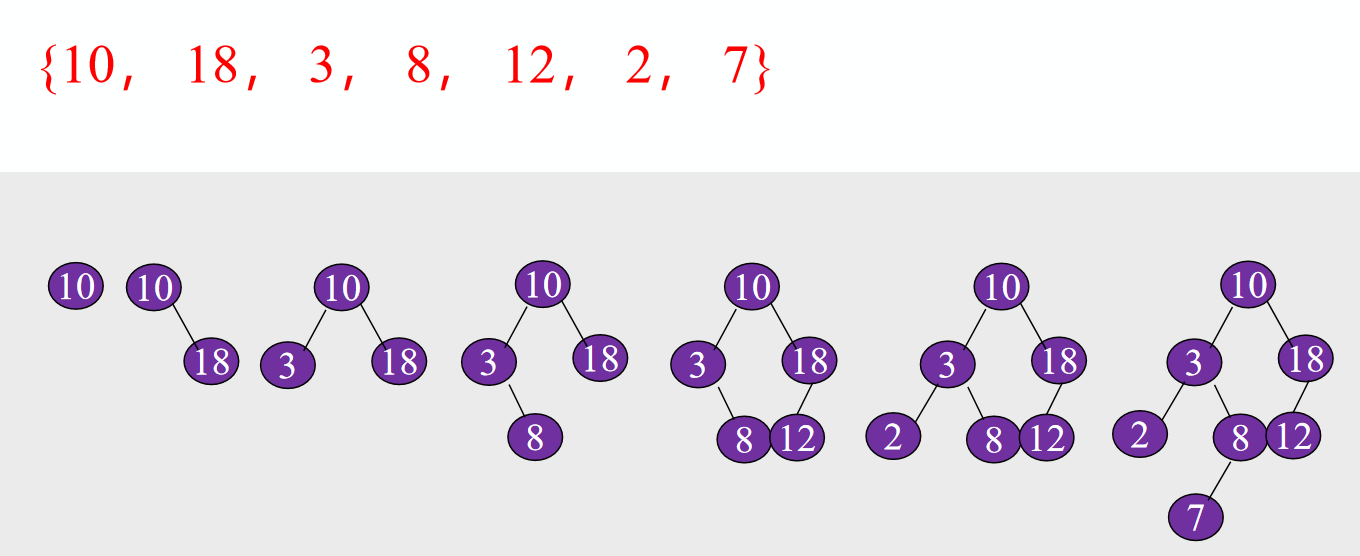
插入&生成
若二叉排序树为空,则插入结点应为根结点;否则,继续在其左、右子树上查找
插入的元素一定在叶结点上
从左往右遍历序列
删除
性能分析
平衡因子:该结点左子树与右子树的高度差
左、右子树是平衡二叉树;所有结点的左、右子树深度之差的绝对值≤1
