目录

  1. 1. 前言
  2. 2. 定义
    1. 2.1. 无向图
    2. 2.2. 有向图
    3. 2.3. 完全图
    4. 2.4. 度数
    5. 2.5. 连通图
    6. 2.6. 生成树
  3. 3. 存储
    1. 3.1. 顺序存储结构——数组表示法（邻接矩阵）
    2. 3.2. 链式存储结构——邻接表
    3. 3.3. 十字链表
  4. 4. 遍历
    1. 4.1. DFS（深度优先搜索）
      1. 4.1.1. 实现——栈
    2. 4.2. BFS（广度优先搜索）
      1. 4.2.1. 实现——队列
  5. 5. 最小生成树
    1. 5.1. Prim算法
    2. 5.2. Kruskal算法
  6. 6. 最短路径问题
    1. 6.1. Dijkstra算法
    2. 6.2. Floyd算法
  7. 7. 拓扑排序
    1. 7.1. AOV网
    2. 7.2. 关键路径——AOE网
↑

LOADING

第一次加载文章图片可能会花费较长时间

要不挂个梯子试试？（x

加载过慢请开启缓存 浏览器默认开启

图

2024/1/14 Basic 数据结构
字数统计: 1.7k字   |   阅读时长: 6分   |   总文章阅读量：次

前言

烂尾了

图 (Graph) 是由若干给定的顶点及连接两顶点的边所构成的图形，

这种图形通常用来描述某些事物之间的某种特定关系。

顶点用于代表事物，连接两顶点的边则用于表示两个事物间具有这种关系。

因为本人已经有离散数学的基础，过于数学的东西这里就不多赘述了

参考：

https://oi-wiki.org/graph/concept/

https://book.itheima.net/course/223/1276707762369208322/1276709341503692801

定义

图是一个二元组Graph=(V,E)，

V是非空集，称为点集（vertex set），对于V中的每个元素，称为顶点（vertex）或节点（node）

E是V中各节点之间边（edge）/ 弧（arc）的集合，称为边集（edge set）

注：这里讨论的都是有限图，即V,E都是有限集合

无向图

E中的每个元素为一个无序二元组(u,v)，称作无向边，简称为边，其中u，v∈V。设e=(u,v)，则u和v称为e的端点

例：

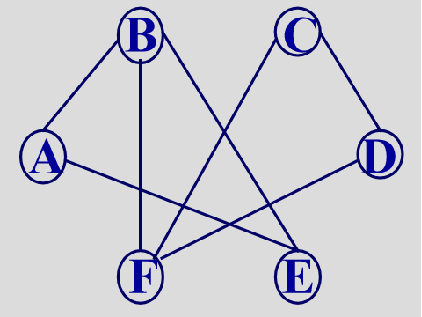
image-20240120005109669

G=(V,E)，V={A, B, C, D, E, F}；

E={(A,B), (A,E),(B,E),(C,D), (D,F),(B,F), (C,F)}

对于n个顶点，e条边的无向图G：

  1. 所有顶点的度之和=2e
  2. 若G是连通图，则最少有 n-1 条边(树)；若e > n-1，则一定有回路
  3. 若G是非连通图，则最多可能有C²n-1条边
  4. 无向完全图共有C²n条边

有向图

E中的每个元素为一个有序二元组(u,v)，也写作u→v，称为有向边或弧。设e=u→v，则u为e的起点（tail），v为e的终点（head）（尾指向头），两者也可称为端点。u是v的直接前驱，v是u的直接后继

例：

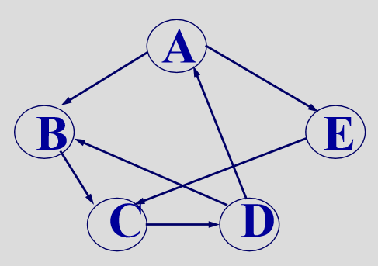
image-20240120005049212

G=(V, E)，V={A, B, C, D, E}；

E={<A,B>,<A,E>,<B,C>,<C,D>,<D,B>,<D,A>,<E,C>}

对于n个顶点，e条弧的有向图G：

  1. 所有顶点的出度之和=入度之和=e

  2. 所有顶点的度之和=2e

  3. 若G是强连通图，则最少有 n 条边 (形成回路)

  4. 有向完全图共有2C²n条边

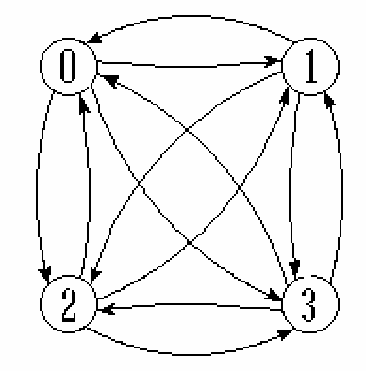
完全图

假设图中有n个顶点，e条边或弧

完全图：含有e=n(n-1)/2条边的无向图

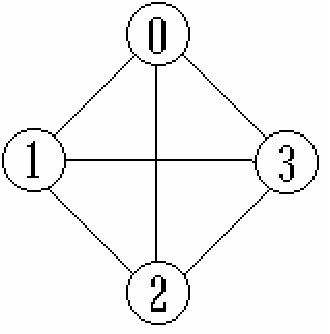
image-20240120005502461

有向完全图：含有e=n(n-1)条弧的有向图

image-20240120005601449

稀疏图：有很少边或弧的图

稠密图：有较多边或弧的图

网：边/弧带权的图

度数

与一个顶点v关联的边的条数称作该顶点的度（degree），记为TD(V)

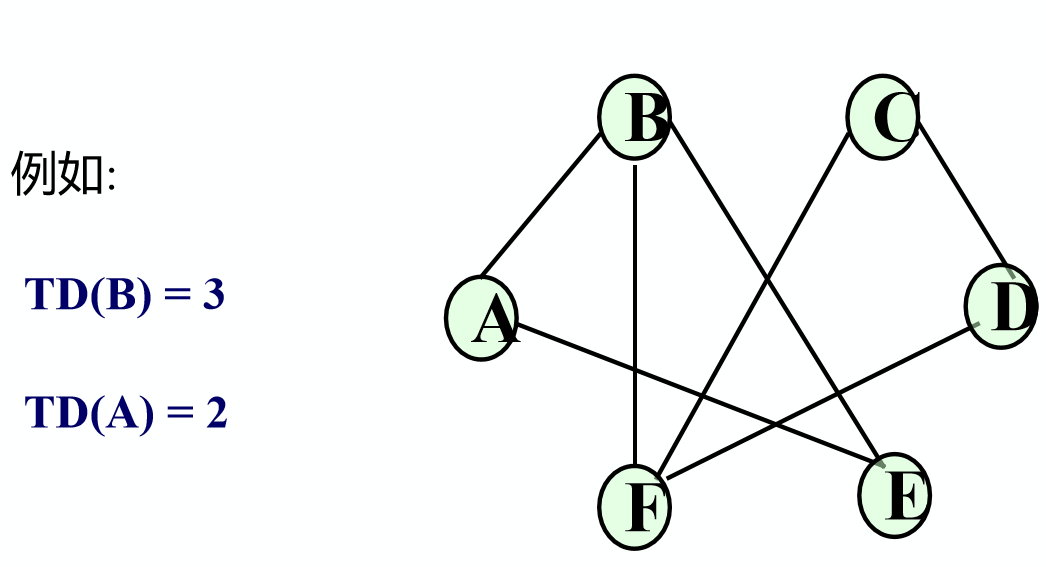
image-20240120005921291

假设图中有n个顶点，e条边或弧，则：

在有向图中，顶点的度等于该顶点的入度与出度之和，所有的顶点的度之和为2e；具有n个顶点的有向图最多有n(n-1)条边

在无向图中，所有顶点的度之和为2e

注：当有向图中仅1个顶点的入度为0,其余顶点的入度均为1，此时是一颗有向树

连通图

在无向图G=(V,E)中，若其中任意两个顶点均连通，则称G是连通图

在有向图G=(V,E)中，节点两两互相可达，则称G是强连通图

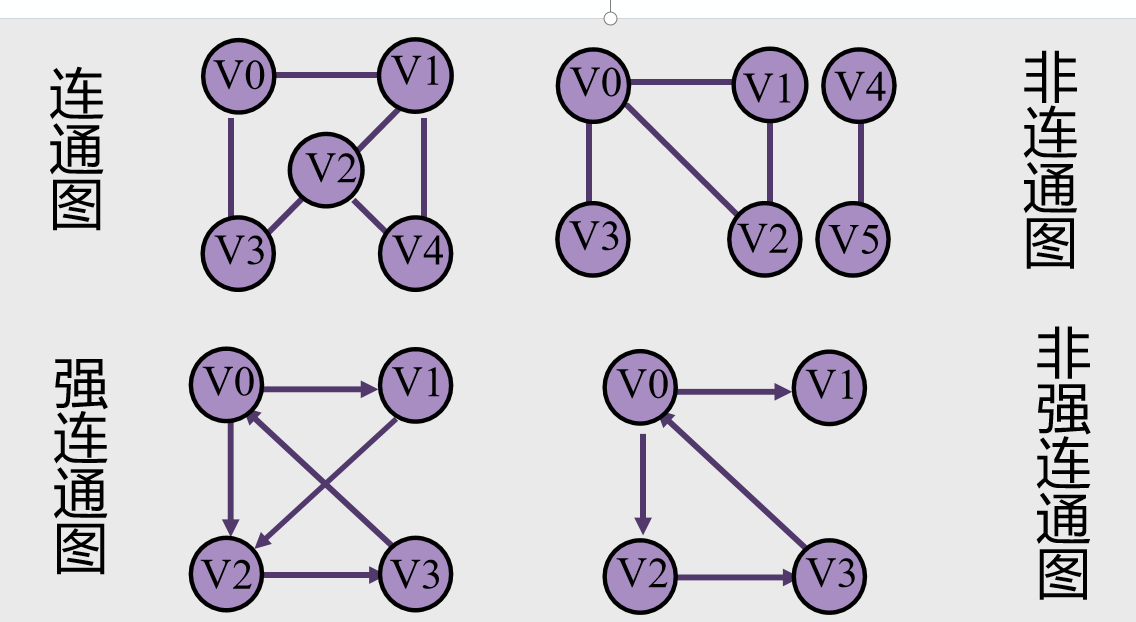
image-20240120010421275

连通分量：无向图G的极大连通子图

强连通分量：有向图G的极大强连通子图

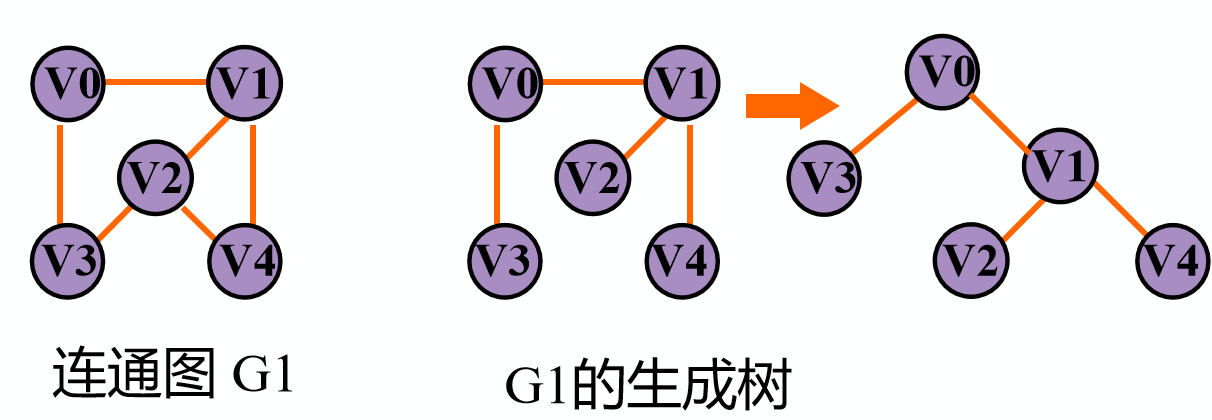
生成树

包含无向图G所有顶点的极小连通子图

  • 极小连通子图：该子图是G的连通子图，在该子图中删除任何一条边，子图不再连通

image-20240120010926596

存储

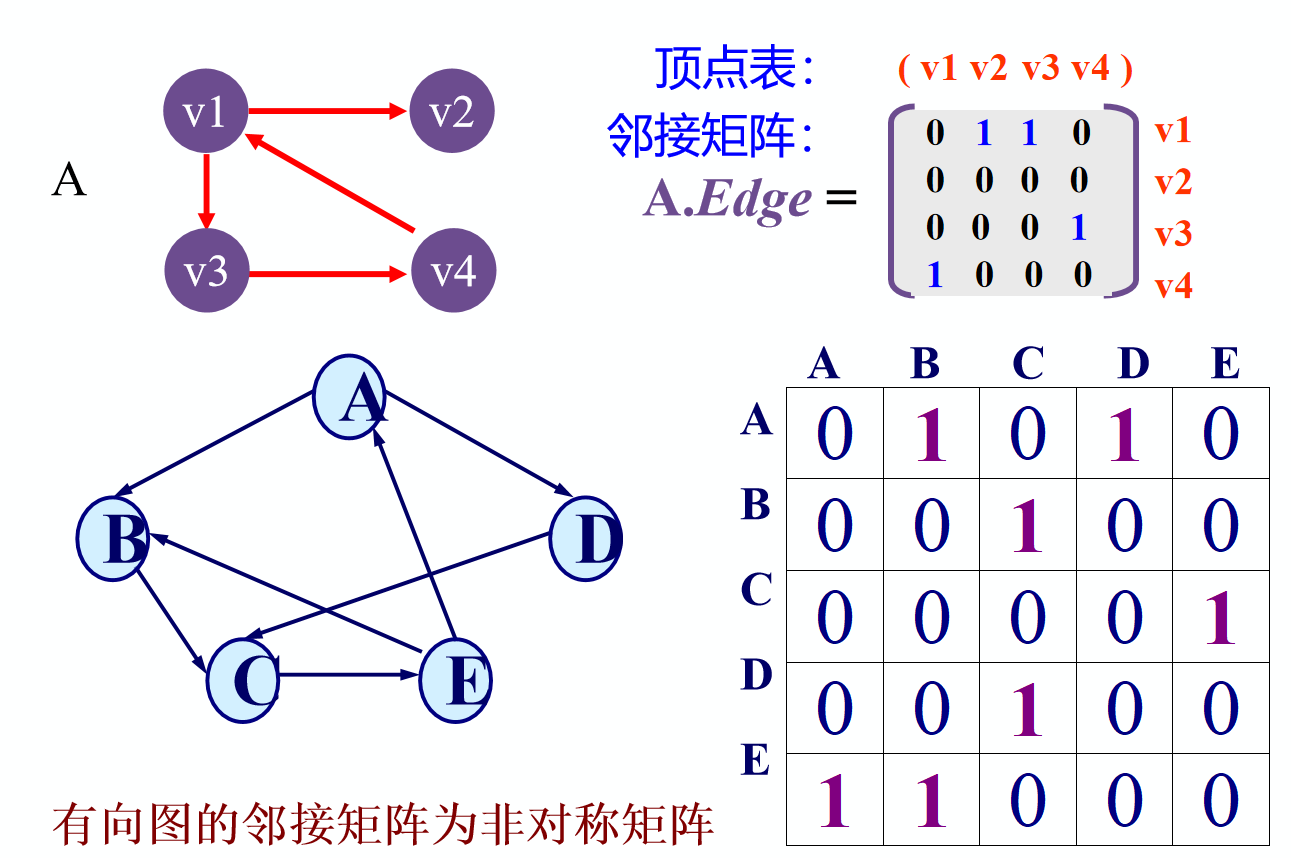
顺序存储结构——数组表示法（邻接矩阵）

建立一个顶点表（记录各个顶点信息）和一个邻接矩阵（表示各个顶点之间关系）

即使用一个二维数组 adj[u][v] 来存边，

其中adj[u][v]如果为1：表示存在u到v的边，如果为0：表示不存在u到v的边

那么根据这个定义创建一个图

#define MAX_VERTEX_NUM 100
typedef struct
{
  int v;   // 顶点数目
  int e;   // 边的数目
  // 存储顶点
  int vexs[MAX_VERTEX_NUM];
  // 存储边
  int edges[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
}Graph;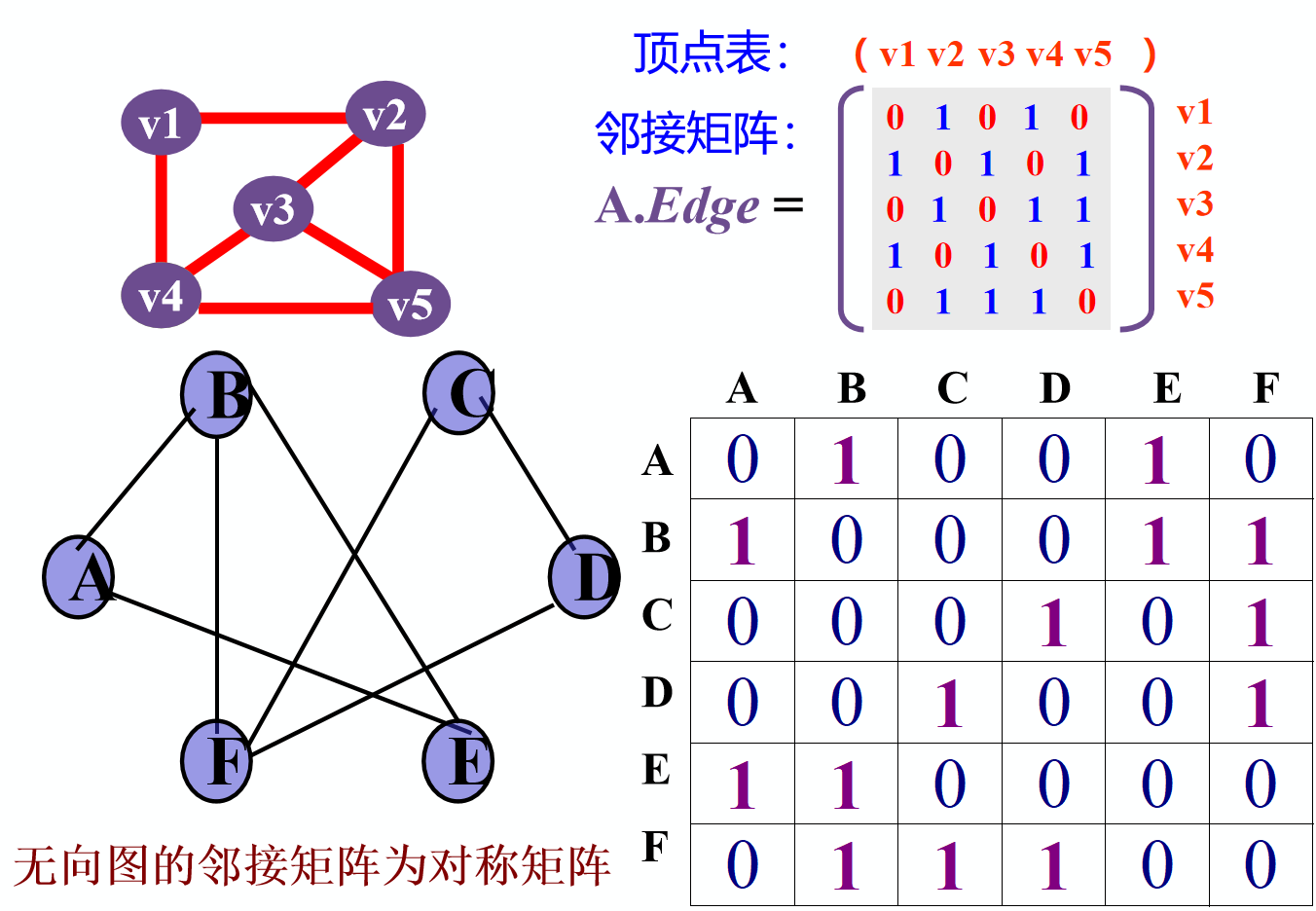

image-20240120011708721

对称矩阵—>同一条边表示了两次

image-20240120011751369

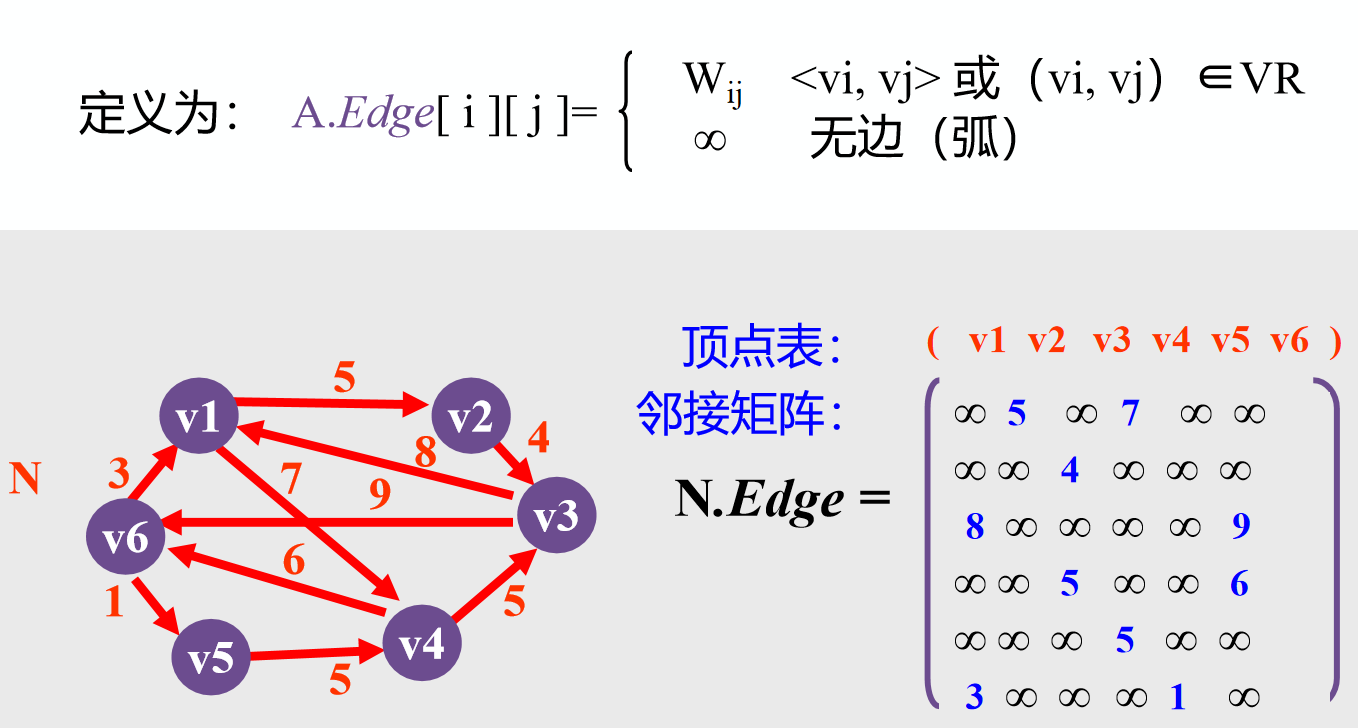
如果是带边权的图，可以在 adj[u][v] 中存储u到v的边的边权

image-20240120011953439

n个顶点的连通图用邻接矩阵表示时，至少有2(n-1)个非零元素

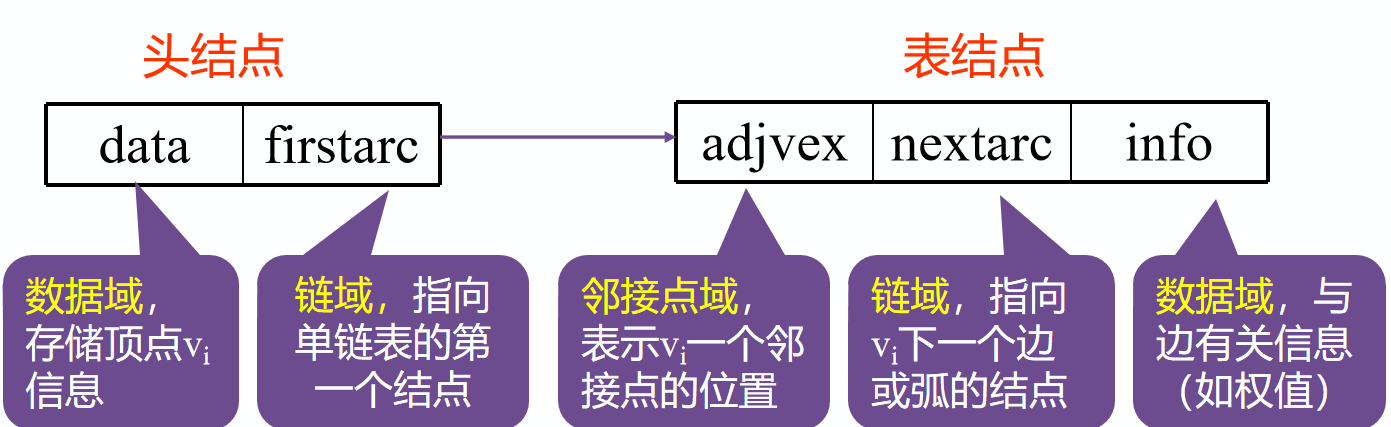
链式存储结构——邻接表

对每个顶点vi建立一个单链表，把与vi有关联的边的信息链接起来，每个结点设为3个域；

每个单链表有一个头结点（设为2个域），存vi信息；每个单链表的头结点另外用顺序存储结构存储。

image-20240120014048213

无向图例：

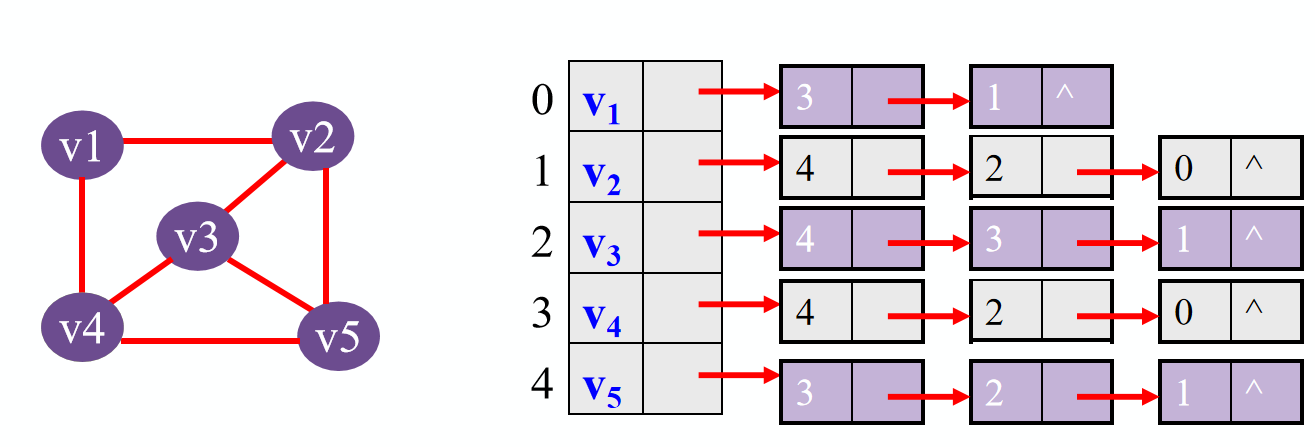
image-20240120014144352

注：邻接表不唯一，因各个边结点的链入顺序是任意的

有向图例：

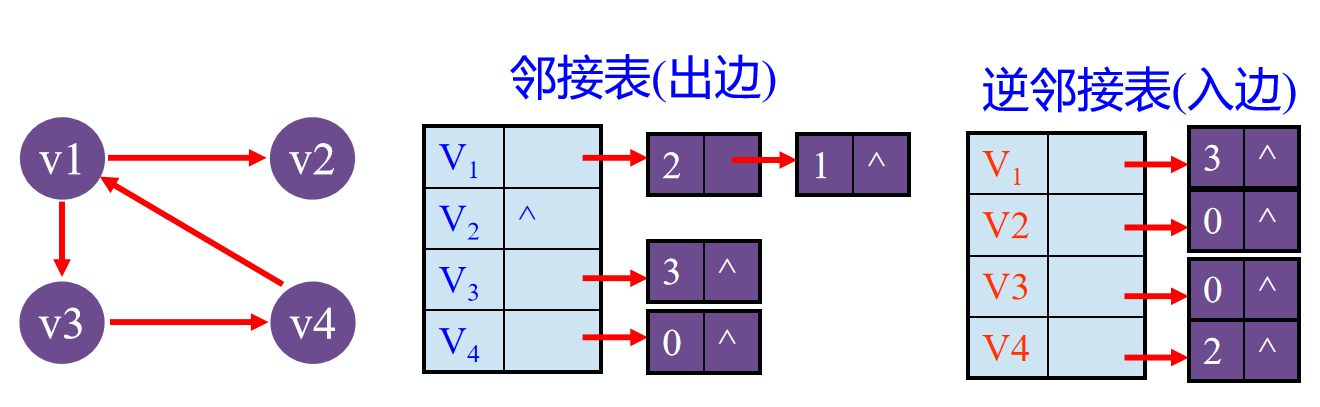
image-20240120014442207

十字链表

遍历

Tips：BFS生成树的树高比DFS生成树的树高小或相等

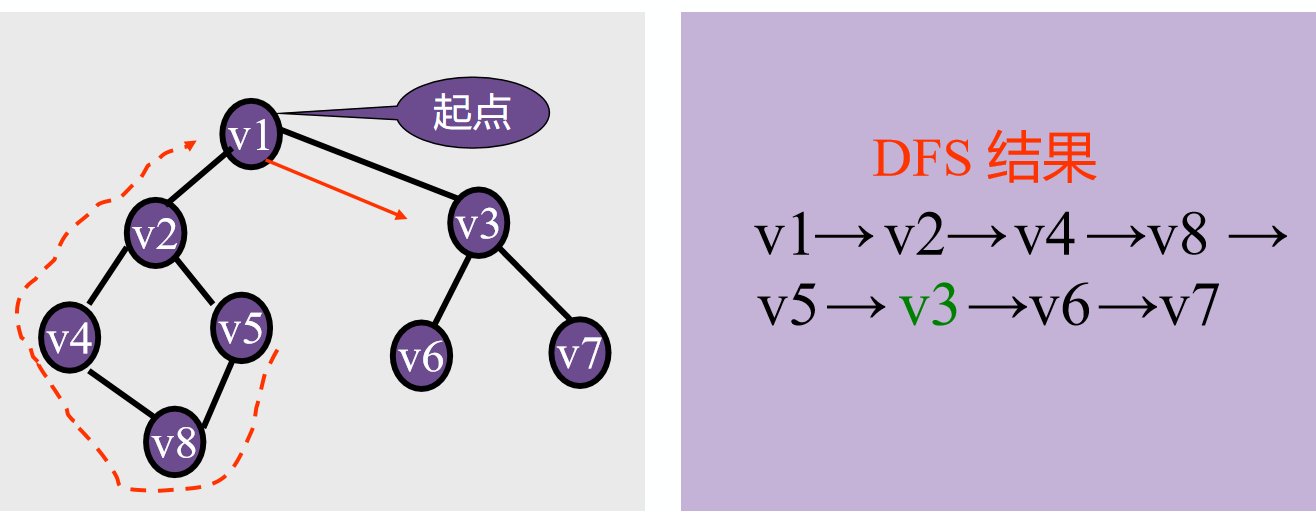
DFS（深度优先搜索）

每次都尝试向更深的节点走

基本思想：仿树的先序遍历过程

特征：递归调用自身

image-20240120014928935

稠密图适于在邻接矩阵上进行深度遍历；稀疏图适于在邻接表上进行深度遍历

实现——栈

使用栈作为遍历中节点的暂存容器

BFS（广度优先搜索）

基本思想：仿树的层次遍历过程

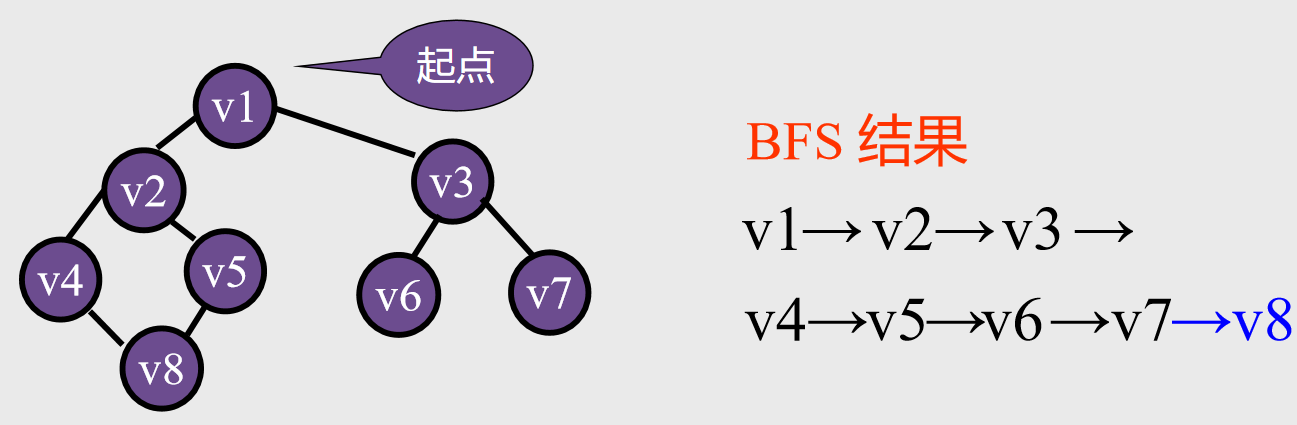
image-20240120015125462

实现——队列

最小生成树

在网的多个生成树中，寻找一个各边权值之和最小的生成树

准则：

  • 必须只使用该网中的边来构造最小生成树
  • 必须使用且仅使用n-1条边来联结网中的n个顶点
  • 不能使用产生回路的边

Prim算法

归并顶点，与边数无关，适于稠密网

从一个结点开始，不断加点

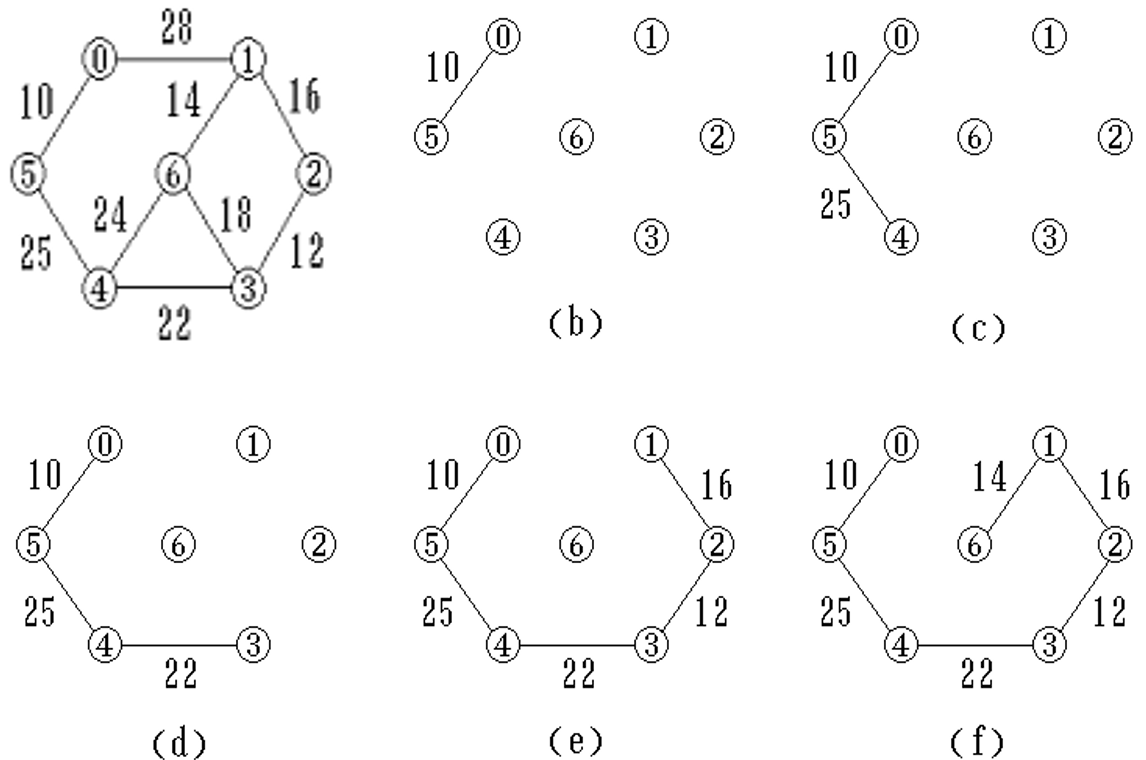
image-20240122221238670

Kruskal算法

归并边，适于稀疏网

从小到大加入边，是个贪心算法

最短路径问题

Dijkstra算法

单源最短路径

Floyd算法

每一对顶点间的最短路径

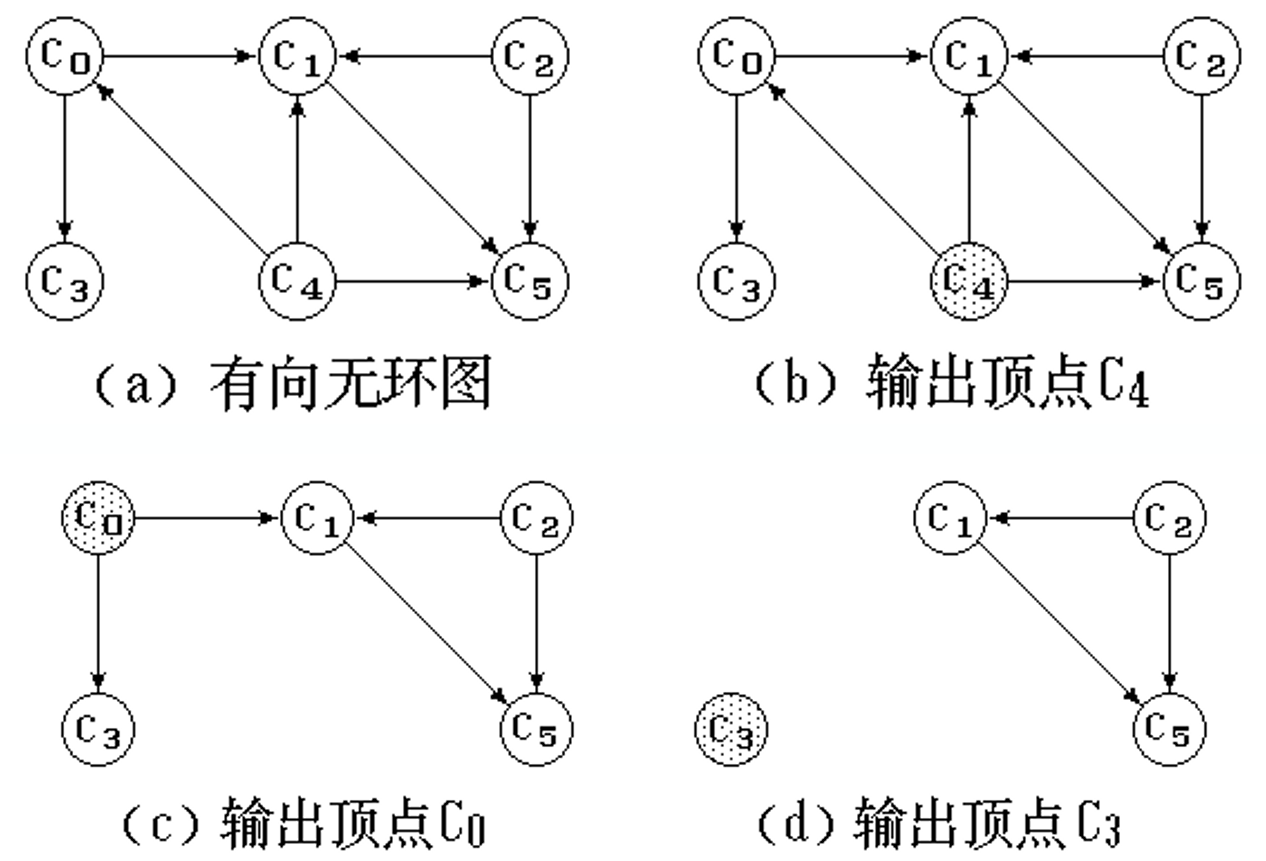
拓扑排序

给一个有向无环图的所有节点排序，拓扑排序的图 <=> 有向无环图

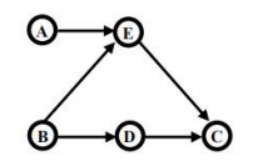
image-20240122224216294

AOV网

用顶点表示活动的网络

算法思想：

  1. 输入AOV网络，令 n 为顶点个数

  2. 在AOV网络中选一个没有直接前驱的顶点, 并输出

  3. 从图中删去该顶点, 同时删去所有它发出的有向边

  4. 重复以上 2、3 步, 直到：

    全部顶点均已输出，拓扑有序序列形成，拓扑排序完成

    或

    图中还有未输出的顶点，但已跳出处理循环。这说明图中还剩下一些顶点，它们都有直接前驱，再也找不到没有前驱的顶点了。这时AOV网络中必定存在有向环。

image-20240122224845091

关键路径——AOE网

用边表示活动的网络