前言

不是想卷算法，只是我姑且还不想在数据结构上挂科（

以清华大学出版社的《数据结构》为基础，结合LeetCode上的《图解算法数据结构》来学习，语言的话我这里就选择python（现在转c了）

啥时候无聊了说不定会拿php写一个（x

链表

oi-wiki上的介绍：https://oi-wiki.org/ds/linked-list/

本篇中不少内容都会出自这里

基础知识

链表是一种用于存储数据的数据结构，通过如链条一般的指针来连接元素。它的特点是插入与删除数据十分方便，但寻找与读取数据的表现欠佳。

线性表

一个线性表是n个数据元素的有限序列

一个数据元素可以由若干个数据项组成，在这种情况下，常把数据元素称为记录，含有大量记录的线性表又称文件

同一线性表中的元素必定具有相同特性

线性表有两种表示方法：顺序表示和链式表示，链式表示即为链表

---

构建链表

单向链表

单向链表中包含数据域和指针域，其中数据域用于存放数据，指针域用来连接当前结点和下一节点。

实现也很简单

class Node:
    def __init__(self, value = None, next = None): 
        self.value = value
        self.next = next

---

双向链表

双向链表中同样有数据域和指针域。不同之处在于，指针域有左右（或上一个、下一个）之分，用来连接上一个结点、当前结点、下一个结点。

可以看出来和单向链表相比多了一个指向前驱的指针

代码实现：

class Node:
    def __init__(self, value = None, left = None, right = None): 
        self.value = value
        self.left = left
        self.right = right

---

向链表中插入数据

单向链表

1. 初始化待插入的数据node
2. 将 node 的 next 指针指向 p 的下一个结点；
3. 将 p 的 next 指针指向 node。

图解如下：

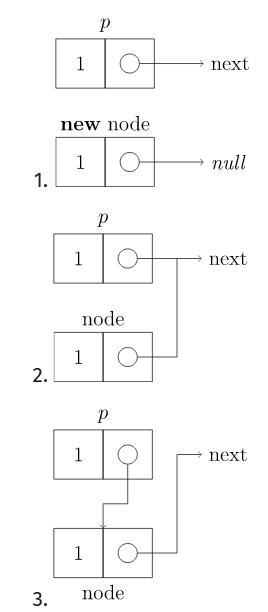
代码实现：

def insertNode(i, p):
    node = Node()
    node.value = i
    node.next = p.next
    p.next = node

---

单向循环链表

将链表的头尾连接起来，链表就变成了循环链表。

由于链表首尾相连，在插入数据时需要判断原链表是否为空：为空则自身循环，不为空则正常插入数据。

1. 初始化待插入的数据 node；
2. 判断给定链表 p 是否为空；
3. 若为空，则将 node 的 next 指针和 p 都指向自己；
4. 否则，将 node 的 next 指针指向 p 的下一个结点；
5. 将 p 的 next 指针指向 node。

除了多了一个判断空表的处理，其它部分和单向链表是一样的

图解如下：图中的第一步对应上面的判断步骤

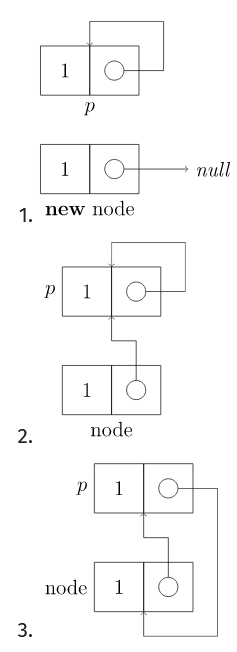
代码实现：

def insertNode(i, p):
    node = Node()
    node.value = i
    node.next = None
    if p == None:
        p = node
        node.next = node
    else:
        node.next = p.next
        p.next = node

---

双向循环链表

在向双向循环链表插入数据时，除了要判断给定链表是否为空外，还要同时修改左、右两个指针。

1. 初始化待插入的数据 node；
2. 判断给定链表 p 是否为空；
3. 若为空，则将 node 的 left 和 right 指针，以及 p 都指向自己；
4. 否则，将 node 的 left 指针指向 p;
5. 将 node 的 right 指针指向 p 的右结点；
6. 将 p 右结点的 left 指针指向 node；
7. 将 p 的 right 指针指向 node。

我这里对5~7画个图图

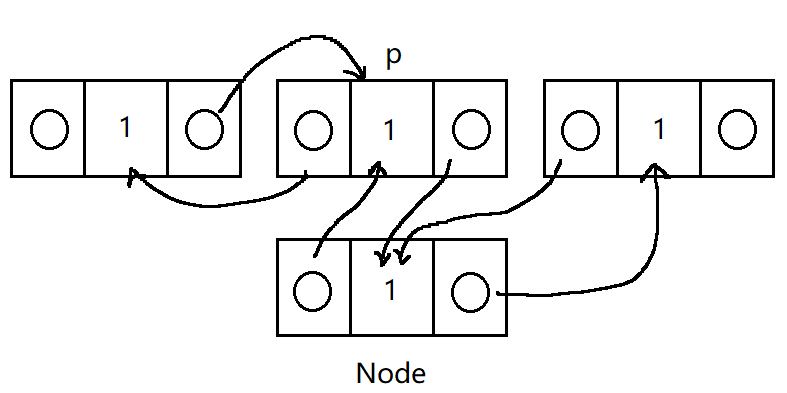
代码实现：

def insertNode(i, p):
    node = Node()
    node.value = i
    if p == None:
        p = node
        node.left = node
        node.right = node
    else:
        node.left = p
        node.right = p.right
        p.right.left = node
        p.right = node

---

从链表中删除数据

单向（循环）链表

设待删除结点为 p，从链表中删除它时，将 p 的下一个结点 p->next 的值覆盖给 p 即可，与此同时更新 p 的下下个结点。

1. 将 p 下一个结点的值赋给 p，以抹掉 p->value；
2. 新建一个临时结点 t 存放 p->next 的地址；
3. 将 p 的 next 指针指向 p 的下下个结点，以抹掉 p->next；
4. 删除 t。此时虽然原结点 p 的地址还在使用，删除的是原结点 p->next 的地址，但 p 的数据被 p->next 覆盖，p 名存实亡。

图解：

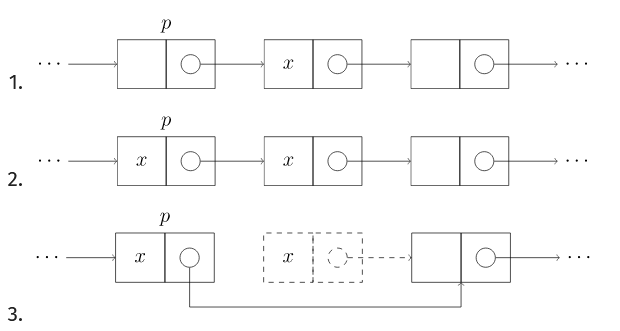
代码实现：

def deleteNode(p):
    p.value = p.next.value
    p.next = p.next.next

双向循环链表

1. 将 p 左结点的右指针指向 p 的右节点；
2. 将 p 右结点的左指针指向 p 的左节点；
3. 新建一个临时结点 t 存放 p 的地址；
4. 将 p 的右节点地址赋给 p，以避免 p 变成悬垂指针；
5. 删除 t。

代码实现：

def deleteNode(p):
    p.left.right = p.right
    p.right.left = p.left
    p = p.right

---

实操（python）

C语言实现的链表是由一个一个的结点构成，每个结点分为数据域和指针域，指针域中存储了其后继结点的地址，通过地址来访问下一个结点，然后一步一步的串联起来形成了一个单链表

但是python中没有指针，怎么办呢？我们知道在python中万物皆对象，所谓的“引用”就是不能运算的指针，那么一个结点可以用类来表示，然后用self.next作为后继节点的引用，就能指向后继节点了

class ListNode:
    def __init__(self, x):
        self.val = x     # 节点值
        self.next = None # 后继节点引用
# 实例化节点
n1 = ListNode(4) # 节点 head
n2 = ListNode(5)
n3 = ListNode(1)

# 构建引用指向
n1.next = n2
n2.next = n3

current = n1  # 指针指向链表的头节点
while current:
    print(current.val)  # 打印当前节点的值
    current = current.next  # 更新指针为下一个节点

这样子就能构成一个节点值为4，后继节点为5的节点4和一个节点值为5，后继结点为1的节点5

然后我们定义一个current指针指向链表的头节点n1，用循环即可将整个链表输出

---

图书整理 I（反转链表）

要求我们逆序返回链表，这里有几种方法

辅助栈法

我们可以遍历链表，创建一个数组，然后反转数组即可

链表只能从前至后访问每个节点，而题目要求倒序输出各节点值，其实本质上就是先入后出的需求，可以用栈来实现

流程：

1. 入栈：遍历链表，将各节点值 push入栈。
2. 出栈：将各节点值 pop出栈，存储于数组并返回。

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None
        
class Solution:
    def reverseBookList(self,head):
        s = []
        while head:
            s.append(head.val)
            head = head.next
        return s[::-1]

---

递归法

利用递归，先递推至链表末端；回溯时，依次将节点值加入列表，即可实现链表值的倒序输出。

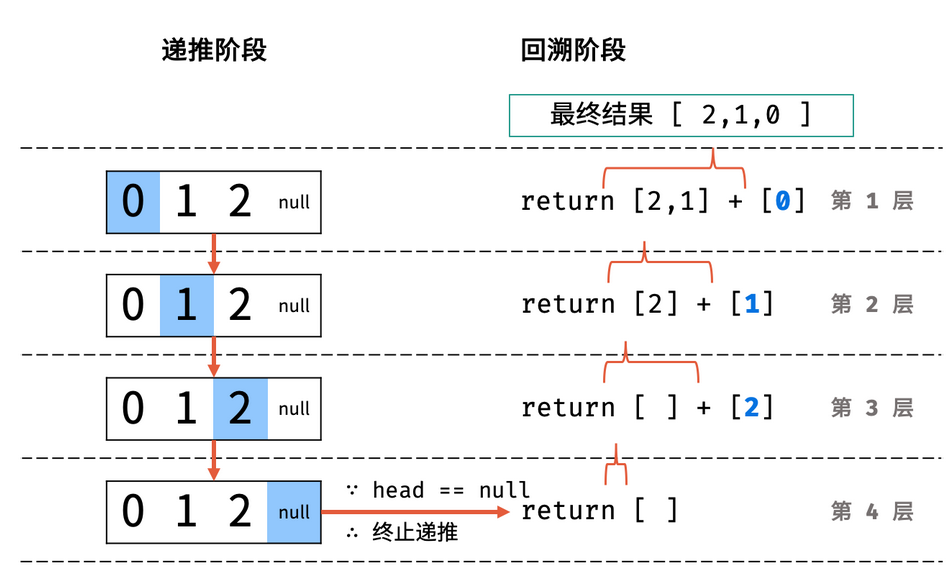
class Solution:
    def reverseBookList(self, head: Optional[ListNode]) -> List[int]:
        return self.reverseBookList(head.next) + [head.val] if head else []

---

删除链表节点

本题删除值为 val 的节点分需为两步：定位节点、修改引用。

1. 定位节点： 遍历链表，直到 head.val == val 时跳出，即可定位目标节点。
2. 修改引用： 删除节点后涉及到前驱节点和后继节点引用的变动，设节点cur的前驱节点为pre，后继节点为cur.next；则执行pre.next = cur.next，即可实现删除cur节点。

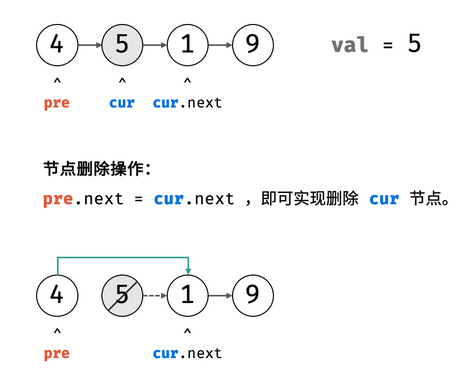
注意，这里要先对第一个节点进行判断是否为val，然后才能设置前驱节点和后继节点

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    def deleteNode(self, head: ListNode, val: int) -> ListNode:
        if head.val == val:
            return head.next
        pre = head
        cur = head.next
        while cur and cur.val != val:
            pre = cur
            cur = cur.next
        if cur:
            pre.next = cur.next
        return head

写的这玩意跑起来耗时有点高，无所谓了（

---

训练计划 III（反转链表）

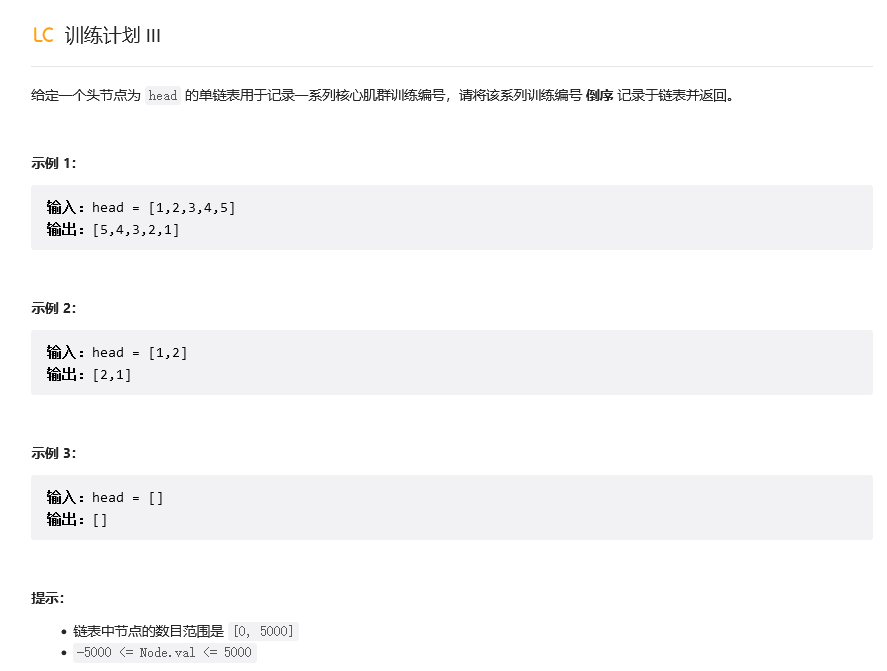
反转链表的基本操作图解：

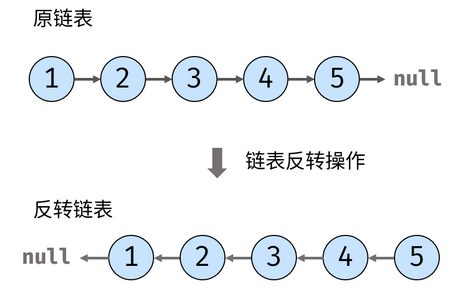
一样是反转链表，那就可以考虑采取和图书整理 I一样的做法，由于辅助栈法需要的复杂度会比较高，所以这里用递归

递归法

利用递归来遍历链表，当越过尾结点来到null后终止递归，在回溯时修改各节点的next引用指向为之前的前驱节点

注意这题的注解和前面那题不一样，这题要返回的是ListNode元素，前面那题是int

那么我们得自己写一个函数来递归反转结点，返回的结果为ListNode元素

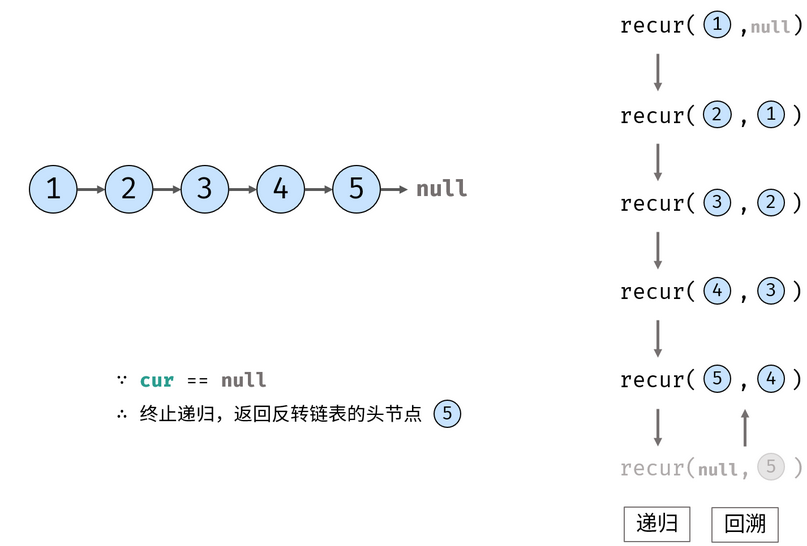
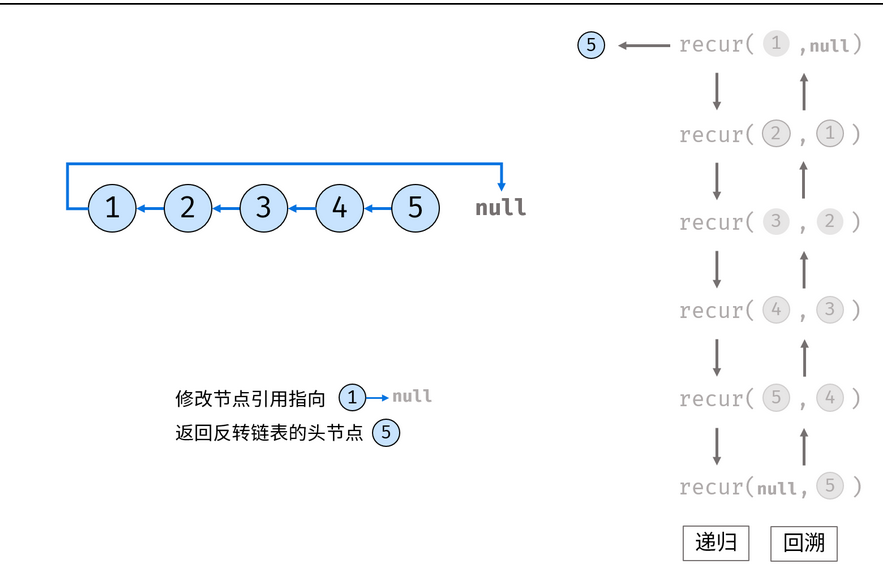
1. 终止条件：当 cur 为空（此时即越过了尾结点指向null），则返回尾节点 pre （即反转链表的头节点）；
2. 递归后继节点，记录返回值（即反转链表的头节点）为 res ；
3. 修改当前节点 cur 引用指向前驱节点 pre ；
4. 返回反转链表的头节点 res ；

图解：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def trainningPlan(self, head: Optional[ListNode]) -> Optional[ListNode]:
        def recur(cur,pre):
            if not cur:
                return pre
            res = recur(cur.next,cur)
            cur.next = pre
            return res

		return recur(head, None)

双指针法

考虑遍历链表，并在访问各节点时修改 next 引用指向，算法流程见注释

图解：

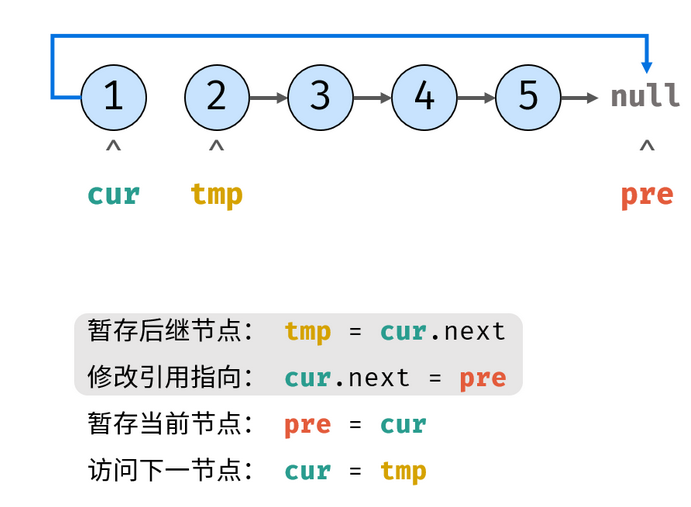
class Solution:
    def trainningPlan(self, head: ListNode) -> ListNode:
        cur, pre = head, None
        while cur:
            tmp = cur.next # 暂存后继节点 cur.next
            cur.next = pre # 修改 next 引用指向
            pre = cur      # pre 暂存 cur
            cur = tmp      # cur 访问下一节点
        return pre

---

训练计划 II

---

数组

基础知识

将相同类型的元素存储于连续内存空间的数据结构，其长度不可变

高级语言中的数组是顺序结构；而这里的数组既可以是顺序的，也可以是链式结构

---

字符串