前言

人话：课程学习笔记（

以一种调动个人积极性的方式学习或许会有所成效？

Ps：本人的博客并不打算使用LateX语法，所以部分公式可能会上个图完事

参考资料：https://oi-wiki.org/math/number-theory

---

第1章：整数的可除性

整除的概念

设a，b是任意两个整数，其中b≠0。如果存在一个整数q使得等式a=q*b成立，就称b整除a或者a被b整除，记作b | a，并把b叫做a的因数，a叫做b的倍数，不能整除就是b ∤ a

根据上面的定义，有：

• 0是任何非0整数的倍数
• 1是任何整数的因数
• 任何非零整数a是其自身的倍数，也是其自身的因数

Tips：不要关心得到的商是多少，只要是整数就是整除，大概就是下面这种形式：

int a = 7;
int b = 2;
printf("%d",a/b);

// 输出：3

定理：

• 整数的传递性：设a，b≠0，c≠0是三个整数，若b|a，c|b，则c|a

  个人翻译：我因数的因数还是我的因数

• 设a，b，c≠0是三个整数。若c|a，c|b，则c|a±b

  证明：

  

• 设a，b，c≠0是三个整数。若c|a，c|b，则对任意整数s、t，有c|(s*a+t*b)。此性质可推广到n个整数的情况（即设整数c≠0，若整数a₁，…，a_n都是整数c的倍数，则对任意n个整数s₁，…，s_n，整数s₁a₁+…+s_na_n是c的倍数）

  证明过程和上面一个类似

• 若a，b都是非零整数。若a|b，b|a，则a=±b

  个人翻译：总之绝对值是相等的

下面的性质由素数拓展出的：

• 设a，b，c是三个整数，且c≠0，如果c|ab，gcd(a,c)=1，则c|b
• 设p是素数，若p|ab，则p|a或p|b。此性质可以推广到n个整数的情况

---

最大公因数&最小公倍数

gcd

一组整数的公因数，是指同时是这组数中每一个数的因数的数。

±1是任意一组整数的公因数。

一组整数的最大公因数，是指所有公因数里面最大的一个。

性质：

• 设a，b，c是三个整数，且b≠0，c≠0，如果gcd(a,c)=1，则gcd(a,b,c)=gcd(b,c)
• 设a₁，…，aₙ，c为整数，如果gcd(aᵢ，c)=1,1≤i≤n，则gcd(a₁...aₙ,c)=1
• 设a，b和u，v都是不全为0的整数，如果a=q*u+r*v，b=s*u+t*v（q，r，s，t都是整数），且q*t+r*v=1，则gcd(a,b)=gcd(u,v)

lcm

一组整数的公倍数，是指同时是这组数中每一个数的倍数的数。

0 是任意一组整数的公倍数。

一组整数的最小公倍数，是指所有正的公倍数里面，最小的一个数。

两者之间的定理

---

素数

设整数n≠0，±1。如果除了显然因数±1和±n外，n没有其他因数，那么，n就叫做素数（或质数或不可约数），否则，n就叫做合数

性质：

• 大于1的整数a是合数，等价于a可以表示为整数d和e（1<d,e<a）的乘积。
• 如果素数p有大于1的约数d，那么d=p。
• 大于1的整数a一定可以表示为素数的乘积。
• 对于合数a，一定存在素数p≤√a使得p|a。
• 素数有无穷多个。
• 所有大于3的素数都可以表示为6n±1的形式。

Eratoshenes筛法（埃氏筛）

设n是正整数，如果对所有的素数p ≤ √n，都有p ∤ n，则n一定是素数

具体的筛法：

因为对于任意一个大于1的正整数 ，不是质数的话其倍数一定不是质数，而质数的倍数也一定不是质数，所以只要从小到大考虑每个数，然后同时把当前这个数的所有（比自己大的）倍数记为合数，那么遍历结束的时候没有被标记的数就是素数了

而要找到直到n为止的所有素数，只要对不超过√n的素数进行筛选就够了

算法如下：

prime = []
def Eratosthenes(n):
    N = n + 1
    is_prime = [False] * N	# 定义一个列表检测是否为素数
    is_prime[0] = is_prime[1] = False	# 排除0和1
    for i in range(2, n + 1):
        is_prime[i] = True	# 先全部设置是素数
    for i in range(2, n + 1):
        if is_prime[i]:
            prime.append(i)	# 如果是素数就添加到prime中
            if i * i > n:	# i的平方大于n就进入下一个循环
                continue
            for j in range(i * i, n + 1, i):
                is_prime[j] = False	# 从i的平方开始遍历i的所有倍数并设置为False


Eratosthenes(100)
print(prime)

运行后得到

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]

很明显，保留下来的都是素数，这个算法中for j in range(i * i, n + 1, i)会依次删掉N=100中2，3，5，7的倍数，2，3，5，7即不大于√N=10的所有素数

素数的平凡判别

我们可以暴力枚举获得素数：

def isPrime(N):
    if N < 2:
        return False
    for i in range(2, N):
        if N % i == 0:
            return False
    return True

但是我们知道对于给定正整数N，如果x是N的因数，那么N/x也是N的因数

那么对每一对（x,N/x），只需要检验其中一个就行了

于是设不大于√N的所有素数为p₁，p₂，…，pₛ，如果N被所有pᵢ除的余数都不为0，即pᵢ∤n，1≤i≤s，则N是素数

算法实现：

def isPrime(N):
    if N < 2:
        return False
    for i in range(2, int(sqrt(N)) + 1):
        if N % i == 0:
            return False
    return True

算术基本定理

算术基本引理：设p是素数，p|a₁a₂，那么p|a₁和p|a₂至少有一个成立

算术基本定理（唯一分解定理）：

素数定理

π(x)用于表示不超过x的素数个数

即随着x的增大，有这样的近似结果

---

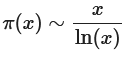
欧几里得除法/辗转相除法

设a，b是两个整数，其中b>0，则存在唯一的整数q，r使得a = q*b+r，0 ≤ r < b

求最大公因数

原理：两个整数的最大公因数（gcd）等于其中较小的数和两数相除余数的最大公因数（gcd）

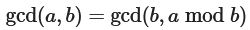
证明：

这里两个数的大小是不会增大的，那么有递归算法实现：

def gcd(a, b):
    if b == 0:
        return a
    return gcd(b, a % b)

递归至 b == 0（即上一步的 a % b == 0）的情况再返回值即可。

迭代算法：

def gcd(a, b):
    while b != 0:
        a, b = b, a % b
    return a

广义欧几里得除法

将两个较大整数的最大公因数计算转化为两个较小整数的计算

算法实现：

print("计算两个非负整数的最大公因数")
num_1 = int(input("请输入第一个非负整数："))
num_2 = int(input("请输入第二个非负整数："))

def Exgcd(num_1, num_2):
    p, q = max(num_1, num_2), min(num_1, num_2)	# 分别对应a，b
    if q == 0:	# 对应rₙ₊₁=0
        return p
    r = p % q	# 取模，然后继续递归求是否为最大公因数
    return Exgcd(q, r)

print("\n%s和%s的最大公因数是%s" % (num_1, num_2, Exgcd(num_1, num_2)))

测试：

手工过程：

Bézout等式（贝祖等式）

从上面的广义欧几里得算法中可以发现我们可以在逐步消去的过程中找到整数s，t使s*a+t*b=gcd(a,b)

那么同样的以上面的例子进行延伸，把这个求出来的最大公因数进行逆推

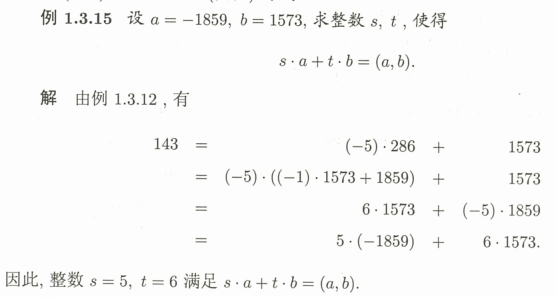
重要推论：a,b互质的充分必要条件是存在整数x,y使ax+by=1

---

整数的表示

b进制

整数n的b进制表示：（运用欧几里得除法）

经典的进制转换：（代码来源：https://plutoacharon.github.io/2020/02/23/Python%E7%AE%97%E6%B3%95%E5%AD%A6%E4%B9%A0-%E4%BB%BB%E6%84%8F%E8%BF%9B%E5%88%B6%E8%BD%AC%E6%8D%A2/）

def f(n, x):
    # n为待转换的十进制数，x为机制，取值为2-16
    a=[0,1,2,3,4,5,6,7,8,9,'a','b','c','d','e','f']
    b=[]
    while True:
        s=n // x  # 商
        y=n % x  # 余数
        b=b+[y]
        if s==0:
            break
        n=s
    b.reverse() # 辗转相除法
    ans = ''
    for i in b:
        ans += str(a[i]) 
    return ans

print("输入原本的进制和要转换的进制，用空格分隔")
A,B = map(int, input().split())
print("输入整数")
n = int(input())
n = int(str(n), A) # int函数可以将A进制的n统一转为十进制
ans = f(n, B)
print(ans)

换算表：

---

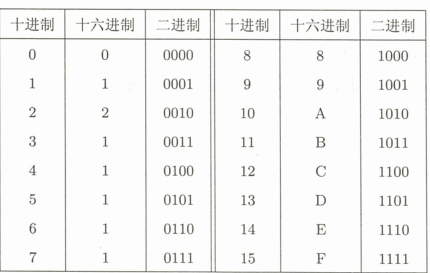
复杂性

即复杂度，符号大O和小o

加法：时间(a+b)=O(max(log₂a, log₂b))，减法同理取最大值

乘法：时间(a+b)=O((log₂a)(log₂b))

除法：时间(a=q*b+r)=O((log₂a)(log₂b))

---

整数分解/分解素因数

将一个正整数写成几个约数的乘积

整数分解定理：

算法：

def breakdown(N):
    result = []
    for i in range(2, int(sqrt(N)) + 1):
        if N % i == 0:  # 如果 i 能够整除 N，说明 i 为 N 的一个质因子。
            while N % i == 0:
                N //= i
                result.append(i)
    if N != 1:  # 说明再经过操作之后 N 留下了一个素数
        result.append(N)
    return result

---

第2章：同余

同余

两个整数a，b，若它们除以正整数m所得的余数相等，则称a，b对于模m同余

以凯撒密码为例：

我们知道凯撒密码是通过移位变换进行加密的，设key（即偏移量）为3，则有

明文字母表：ABCDEFGHIJKLMNOPQRSTUVWXYZ
密文字母表：DEFGHIJKLMNOPQRSTUVWXYZABC

此时我们可以用一个数学函数来表示这个变换a ↔ (a+3)mod 26

由此可以得到算法实现如下（这里仅展示字母全为大写的情况）：

def en(text, shift):
    cipher = ""
    for char in text:
        shift_char = chr(((ord(char) - ord('A')) + shift) % 26 + ord('A'))
        cipher += shift_char
    return cipher

print(en("HELLOWORLD", 3))

注：根据整除的性质，上面的同余式也等价于

同余的性质：

主要是自反性、对称性、传递性和线性运算

剩余类/同余类

全体整数按照对一个正整数的同余关系（等价关系）而分成的类

模m的a的剩余类：

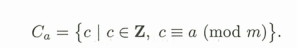
其中的任意一个数都叫做该类的剩余或代表元

求解剩余类的算法：

def find_congruence_class(number, modulus):
    congruence_class = []
    for num in range(modulus):
        if num % modulus == number % modulus:	# 遍历小于模的整数对模取余，与传入的整数对模取余进行比较（即是否同余）
            congruence_class.append(num)
    return congruence_class

number = int(input("请输入一个整数："))
modulus = int(input("请输入模数："))
congruence_class = find_congruence_class(number, modulus)
print(f"{number} 的模 {modulus} 的剩余类是：{congruence_class}")

完全剩余系

m个整数，其中的任何两个数都不在同一个剩余类里

充要条件：它们模m两两不同余

---

欧拉函数φ(N)

小于等于n和n互质的数的个数

性质：

算法实现：

求一个数的话，只要根据定义，在质因数分解的同时求出来即可，即质因数的倍数均不与这个数互质

import math
def euler_phi(n):
    ans = n
    for i in range(2, math.isqrt(n) + 1):
        if n % i == 0:	# 找到质因子
            ans = ans // i * (i - 1)	# 得到互质的个数
            while n % i == 0:
                n = n // i
    if n > 1:
        ans = ans // n * (n - 1)
    return ans

费马小定理

若p为素数，gcd(a,p)=1，则aᵖ⁻¹≡1(mod p)

对于任意整数a，有aᵖ≡a(mod p)

欧拉定理

若gcd(a,m)=1，则aᵠ⁽ᵐ⁾≡1(mod m)

Wilson定理

设p是一个素数，则(p-1)!≡-1(mod p)

模重复平方计算法

在计算bⁿ(mod m)时，

由同余的性质可知：

• ab (mod m) =(a mod m) (b mod m) (mod m)
• a² (mod m) =(a mod m)²(mod m)
• aⁿ(mod m) =(a mod m)^n-1(a mod m) (mod m)

在m很小的时候，上述的方法是可行的，但是当m，n都很大的时候，需要计算n-1次模乘（平方），是不可行的

可以把指数n写成二进制，即

n = n₀ + n₁² + ⋯ + n_k-1^2k-1 , n i∈{0, 1}, i = 0, 1, … ,k−1

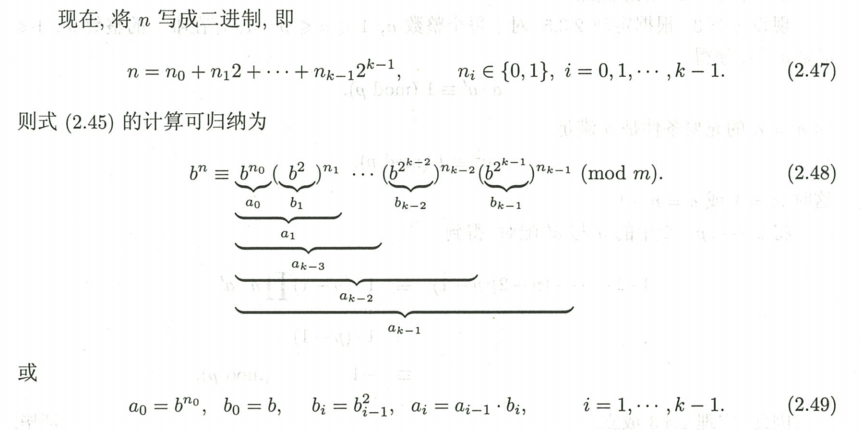
把指数转换成二进制的形式，再按位拆成多组底数相同的指数幂相乘

接下来就是对每组指数幂取模进行同余运算

具体算法：

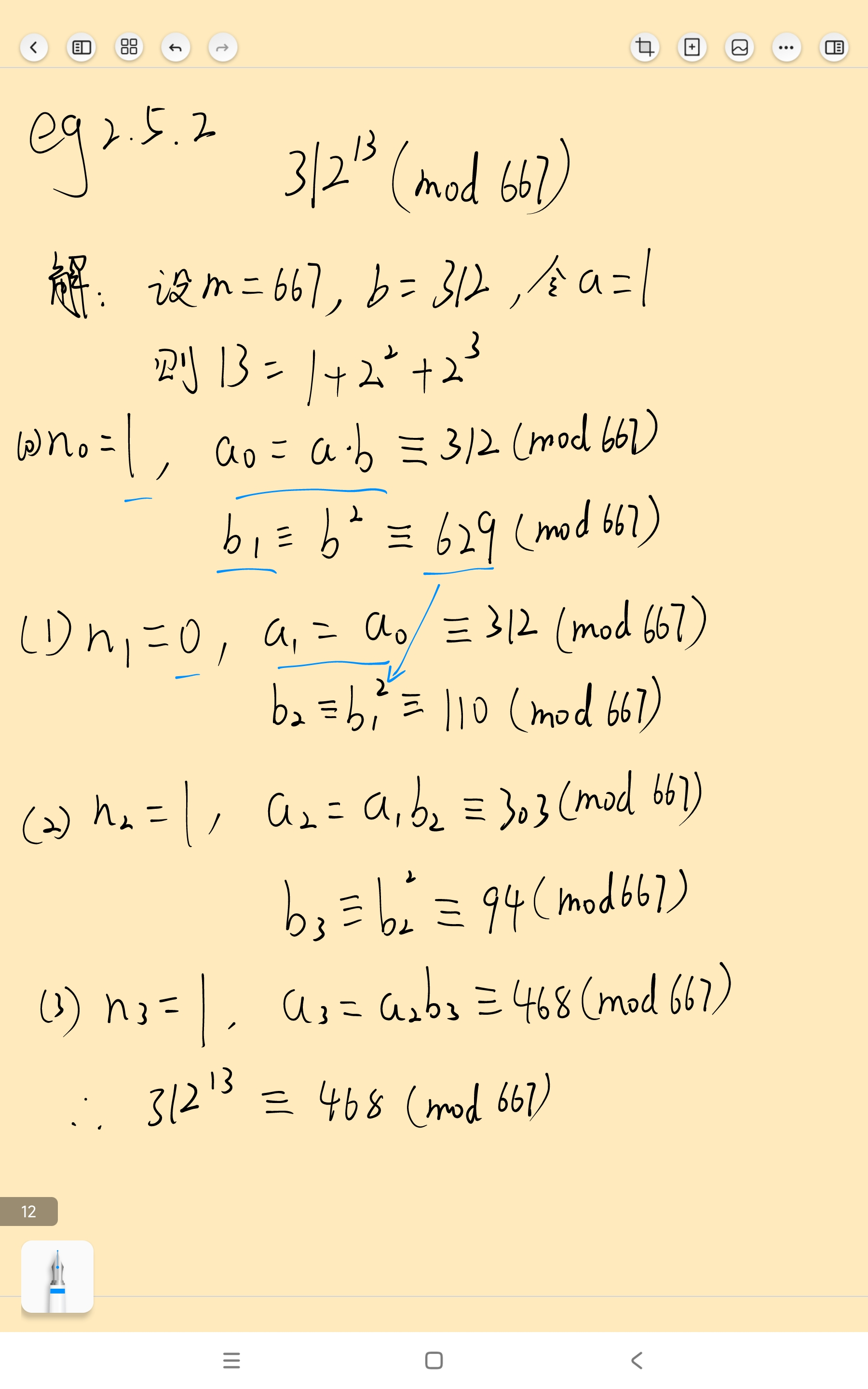
def fast_mod(x, n, m):
    a = 1
    b = x	# 底数
    while True:
        temp = n	# 决定循环次数，循环次数为指数转化成二进制的位数，即计算的次数
        if n % 2 == 1:	# 对应算法步骤里n=1时才进行的运算
            a = a * b % m
        b = b * b % m
        n = n // 2
        if temp < 1:
            return a

---

第3章：同余式

一次同余式

即同余下对多项式的求解

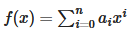
则f(x) ≡ 0(mod m)，叫做模m同余式

次数：若 a_n ≢ 0(mod m)，则n叫做f(x)的次数，记为deg f，那么就可以叫做模m的n次同余式

同余式求解：

1. 求解归约：f(x)(mod m) ← f(x)(mod p^α) ← f(x)(mod p)
2. 解的存在性：m是一个正整数，a是一个满足m ∤ a的整数，ax ≡ b(mod m)有解的充要条件是(a,m) | b
3. 解的个数
4. 具体求解

逆元求解

存在 a’ 使a * a' ≡ a' * a ≡ 1(mod m)成立，则a叫做模m的可逆元，a’叫做a的模m逆元

记作 a’ = a^-1(mod m)

所以同余式的解可写成 x ≡ a^-1(mod m)

扩展欧几里得算法求解

1. 用欧几里得除法计算(a, m), 判断(a, m) | b 是否成立.

2. 若成立,，用广义欧几里德除法求出同余式 a₁x≡1 (mod m₁)的一个解x≡x₀ (mod m₁), 其中a1 =a/(a, m), m1=m/(a, m).

3. 然后求ax ≡ b(mod m)的一个特解 y ≡ x₀b/(a,m)(mod m)

4. 最后写出全部解 x = y + t*m/(a,m) (mod m)，t=0,1,…,(a,m)-1

---

中国剩余定理（CRT）

引入——”物不知数“问题

求满足以下条件的整数：除以3余2，除以5余3，除以7余2

这个问题可以用同余式组来表示：

def CRT(k, a, r):
    n = 1; ans = 0
    for i in range(1, k + 1):
        n = n * r[i]
    for i in range(1, k + 1):
        m = n // r[i]; b = y = 0
        exgcd(m, r[i], b, y) # b * m mod r[i] = 1
        ans = (ans + a[i] * m * b % n) % n
    return (ans % n + n) % n

---

第4章：二次同余式与平方剩余

二次同余式：关于未知数的二次多项式的同余方程

一般二次同余式

一般形式

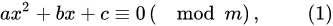
平方剩余/二次剩余

一个整数x对另一个整数m的二次剩余指x的平方除以m得到的余数a

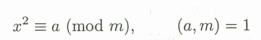
否则就是平方非剩余

---

勒让得符号

设p为素数

如果勒让得符号(a|p) = 1，a便称为二次剩余，此时x²≡a(mod p)有解

如果(a|p) = −1，则a称为二次非剩余，此时x²≡a(mod p)无解

定理：欧拉判别法则

---

第5章：原根与指标

设m > 1是整数，a是与m互素的正整数，则使得 a^e ≡ 1 (mod m) 成立的最小正整数 e 叫做 a 对模 m 的指数，记作 ord_m(a)

a 对模 m 的指数为 φ(m)，则 a 叫做模 m 的原根

求是否为原根：

注：求得 -1 的需要对 ord_m 进行一次平方，即化成 1 才行

---

第8章：群

群

结合法/运算

设 S 是一个非空集合，那么 S x S 到 S 的映射就叫做 S 的结合法或运算

以下面这个映射为例：

S x S -> S
(a,b) -> ab

对于这个映射，元素对 (a,b) 的像叫做 a 与 b 的乘积，即这里的ab，这个结合法就可以叫做乘法，而这里的 S 叫做代数系

这个结合法也可以叫做加法，那么ab表示的就是：元素对 (a,b) 的像叫做 a 与 b 的和

运算规则：

1. 结合律：(ab)c = a(bc)，满足结合律的群叫半群
2. 单位元：如果 S 中有一个元素e，使得对 S 中所有元素a，都有ea = ae = a，那么 e 为 S 中的单位元
3. 可逆元：aa' = a'a = e，此时a为 S 中的可逆元，a'为a的逆元，通常记作 a^-1（S的结合法做加法时这里为 -a ）
4. 交换律：ba = ab

---

群的定义

设G是一个具有结合法的非空集合，则G叫做一个群

其结合法满足下列条件：

1. 结合律
2. 单位元
3. 可逆性

当 G 的结合法写作乘法时，称为乘群

当 G 的结合法写作加法时，称为加群

群 G 的元素个数叫做群 G 的阶，记为|G|，当|G|为有限数时，G叫做有限群；否则是无限群

如果群 G 中的结合法还满足交换律，那么G叫做一个交换群或 Abel 群

---

子群

设 H 是群G 的一个子集合，如果对于群G 的结合法，H 成为一个群，那么 H 就叫做群G 的子群，记作 H≤G

平凡子群：H = {e} 和 H = G

真子群：H 不是 G 的平凡子群

H 是群G 的子群的充要条件：对任意的 a,b ∈ H，有 ab^-1 ∈ H

多个子群的交集：一定是子群，但是多个子群的并集不一定是子群

---

子群的生成

存在一个元素 g ∈ G，对于每一个元素 a ∈ G，都有一个相应的 i ∈ I，能把 a 表示成 gⁱ，则称 G 为循环群，g 称为循环群的生成元

---

第10章：环与理想

环

设 R 是具有两种结合法（加法和乘法）的非空集合，如果下列条件成立，则 R 叫做环：

1. R 对于加法构成一个交换群
2. 结合律：对于任意的 a , b , c ∈ R，有 (ab)c = a(bc)，即R对于乘法构成一个半群
3. 分配律：对于任意的 a , b , c ∈ R，有 (a + b)c = ac + bc和 a(b + c) = ab + ac，即乘法在加法上可以分配

交换环：在上面的基础上满足对任意的 a, b ∈ R，有 ab = ba

有单位元环：R中有一个元素 e = 1_R 使 a1_R = 1_Ra = a

整环及域

整环：R 中有单位元，但没有零因子

域：交换环 K 中有单位元，且每个非零元都是可逆元，即 K 对于加法构成一个交换群，K = K \ {0} 对于乘法构成一个*交换群